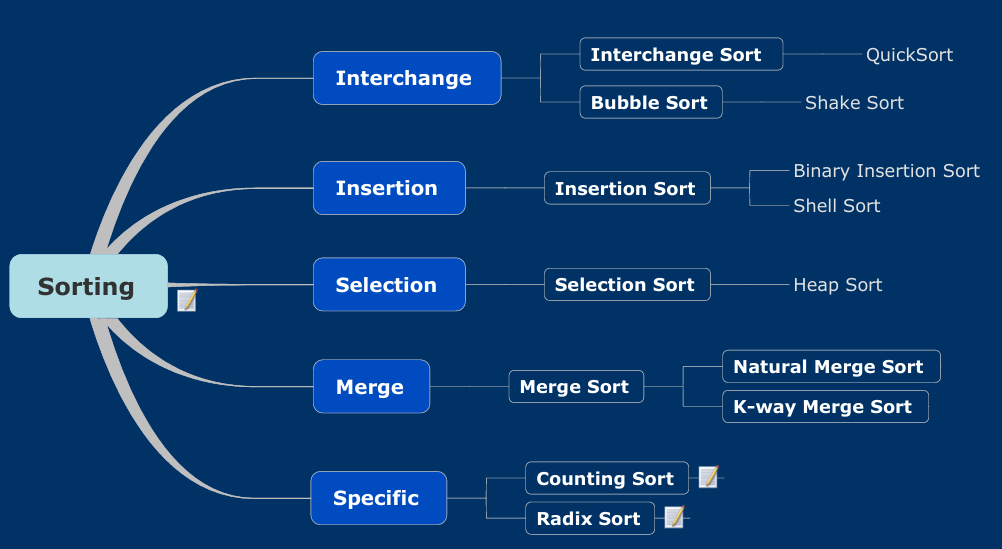
DSA #2 - Các thuật toán sắp xếp

Bài viết về các thuật toán sắp xếp dựa trên sơ đồ sau:

Nhóm Interchange

Interchange sort

Khái niệm Interchange sort

Ý tưởng thuật toán: Dựa trên sự hoán đổi các cặp nghịch thế. Khái niệm cặp nghịch thế như sau:

• Xét một mảng a[0], a[1], ..., a[n - 1], nếu có i < j và a[i] > a[j] thì ta gọi đó là một cặp nghịch thế.

• Một mảng đã sắp xếp sẽ không tồn tại cặp nghịch thế, vì a[0] < a[1] < ... < a[n - 1]. Thuật toán Interchange sort dựa trên sự triệt tiêu các cặp nghịch thế.

Cách hoạt động: Sử dụng hai biến chỉ số i và j, duyệt từ đầu đến cuối mảng, vòng lặp i lồng bên ngoài vòng lặp j.

• Với mỗi lượt lặp, i sẽ lần lượt đi từ phần tử a[0] đến a[n - 2].

• j sẽ chạy từ i + 1 tương ứng đến a[n - 1].

• Nếu phát hiện a[i] và a[j] là cặp nghịch thế, hoán đổi hai phần tử này.

• Sau mỗi vòng lặp, sẽ có một phần tử được đưa về đúng vị trí ở đầu mảng (vì các phần tử ở phía sau mà nhỏ thì đều bị hoán đổi về trước vì nó tạo nên cặp nghịch thế).

Mô phỏng: (Nguồn: CodeLearn)

Hàm Interchange sort

void interchange(int a[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            if (a[i] > a[j])
                swap(a[i], a[j]);
        }
    }
}

Độ phức tạp thuật toán Interchange sort

Đều là $O(n^2)$ cho cả 3 trường hợp tốt nhất, trung bình và xấu nhất.

Số lượt lặp cần thực hiện trong cả 3 trường hợp đều là $\frac{n(n-1)}{2}$, chỉ khác ở số thao tác hoán đổi phần tử.

Quick Sort

Khái niệm Quick sort

Ý tưởng thuật toán: Dựa trên ý tưởng về array partition. Có một phần tử được chọn làm pivot, và sắp xếp các phần tử khác dựa trên pivot đó: nếu bé hơn pivot, phần tử đang xét được đặt về bên trái pivot, ngược lại thì đặt về bên phải. Sau mỗi bước partition, sẽ có một phần tử được đặt đúng vị trí. Thực hiện đệ quy với các mảng con, sẽ sắp xếp được toàn mảng.

Cách chọn pivot: Có nhiều cách có thể được sử dụng để chọn phần tử pivot. Việc này hoàn toàn phân biệt với các phương pháp array partition (được đề cập bên dưới). Các cách chọn pivot phổ biến:

• Ngẫu nhiên: hiệu quả trong việc tránh trường hợp xấu nhất $O(n^2)$.

• Median-of-three: chọn ba phần tử (đầu, giữa, cuối của mảng con) và tìm giá trị trung vị của ba phần tử đó. Cũng giúp tránh được trường hợp xấu nhất $O(n^2)$ nhưng phức tạp hơn random một chút.

• Chọn phần tử đầu tiên/cuối cùng: Cực kỳ đơn giản chỉ với một dòng lệnh, nhưng sẽ dễ bị rơi vào trường hợp xấu nhất $O(n^2)$, vì mỗi lần partition sẽ làm mảng bị chia thành hai phần là $0$ phần tử và $N - 1$ phần tử còn lại, với trường hợp dữ liệu đầu vào đã được sắp xếp hoặc ngược sắp xếp.

• Chọn phần tử ở giữa mảng (ví dụ: arr[(left + right) / 2]): hiệu quả trong việc tránh trường hợp xấu nhất $O(n^2)$.

Array partition:

Là một sự sắp xếp mảng sao cho:

\[\{a_1, \ldots, a_{s-1}\} \leq a_{s} \leq \{a_{s+1}, \ldots, a_{n}\}\]

Sau bước partition, phần tử $a_s$ được đặt đúng vị trí.

Ta có thể tiếp tục sắp xếp hai mảng con bên trái và bên phải của $a_s$ với cách tương tự.

Hàm QuickSort có thể được viết đơn giản dựa trên ý tưởng về partition. Pseudo code:

QuickSort(a[], left, right)
{
    if (left < right) {
        s = partition(a, left, right);
        QuickSort(a, left, s);
        QuickSort(a, s + 1, right);
    }
}

Hàm partition:

Hoare partition:

Ban đầu, chọn pivot p = a[left]. Sử dụng hai biến chỉ số i và j để duyệt từ đầu và cuối mảng.

\[\begin{array}{|c|c|c|c|c|c|} \hline p & \text{all } \leq p & \geq p & \cdots & \leq p & \text{all } \geq p \\ \hline & & \rightarrow\ i & & \leftarrow\ j & \\ \hline \end{array}\]

• Biến i duyệt từ đầu đến cuối mảng, dừng lại khi gặp a[i] >= p.

• Biến j duyệt từ cuối đến đầu mảng, dừng lại khi gặp a[j] <= p.

Khi duyệt xong, sẽ có ba trường hợp về vị trí tương đối giữa i và j:

• i < j: Hoán đổi hai phần tử a[i] và a[j], sau đó tăng giá trị của i lên 1, giảm giá trị của j xuống 1 và tiếp tục duyệt.

• i > j: Lúc này ta thấy vị trí j chính là vị trí đúng của phần tử pivot. Hoán đổi pivot và a[j], trả về j từ hàm.

\[\begin{array}{|c|c|c|c|c|} \hline 5 & \text{all are } \leq p & 4 & 6 & \text{all are } \geq p \\ \hline & & \underset{j}{\leftarrow} & \underset{i}{\rightarrow} & \\ \hline \end{array}\]

• i = j: Lúc này a[i] = a[j] = pivot, vì vậy vị trí i = j chính là vị trí chính xác của phần tử pivot, không cần thay đổi mảng, chỉ cần trả về i hoặc j.

Pseudo code:

Partition(a[], left, right)
{
    while (true)
    {
        pivot = a[left];
        i = left - 1;
        j = right + 1;

        do i++; while (a[i] < pivot);
        do j--; while (a[j] > pivot);

        if (i >= j) return j;
        swap(a[i], a[j]);
    }
}

Lomuto partition:

Chọn phần tử cuối cùng của mảng làm pivot. Sử dụng hai biến vị trí i và j để duyệt qua mảng.

• Biến i luôn lưu vị trí của phần tử gần pivot nhất mà a[i] <= pivot. Điều này giúp bước hoán đổi phần tử swap(a[i + 1], a[right]) luôn hoán đổi đúng phần tử > pivot.

• Biến j là biến chạy từ đầu đến phần tử kế cuối của mảng.

Pseudo code:

Partition(a[], left, right)
{
    pivot = a[right];
    i = left - 1;
    for (int j = left; j <= right - 1; j++)
    {
        if (a[j] <= pivot)
        {
            i++;
            swap(a[i], a[j]);
        }
    }
    swap(a[i + 1], a[right]);
    return i + 1;
}

Hàm Quick sort

int hoare_partition(int a[], int left, int right)
{
    int p = a[left];
    int i = left - 1;
    int j = right + 1;

    while (true)
    {
        do i++; while (a[i] < p);
        do j--; while (a[j] > p);
        if (i >= j) return j;
        swap(a[i], a[j]);
    }
}

int lomuto_partition(int a[], int left, int right)
{
    int p = a[right];
    int i = left - 1;

    for (int j = left; j <= right - 1; j++)
    {
        if (a[j] <= p)  // i phai luon nam giu phan tu gan nhat <= p
                        // luc do buoc swap(a[i+1], a[right]) se swap dung phan tu lon hon p
        {
            i++;
            swap(a[i], a[j]);
        }
    }
    swap(a[i + 1], a[right]);
    return i + 1;
}

void quickSort(int a[], int l, int r)
{
    if (l < r)
    {
        int s = hoare_partition(a, l, r);
        quickSort(a, l, s);
        quickSort(a, s + 1, r);
    }
    else return;
}

Độ phức tạp thuật toán Quick Sort

Trong hàm quickSort, hàm này thực hiện chia mảng thành các mảng con, nên ta có số bước chia mảng cần thiết là $O(\log_{2}n)$.

Với mỗi bước phân hoạch, ta cần duyệt qua toàn bộ mảng, vậy độ phức tạp cho thao tác này là $O(n)$.

Vậy độ phức tạp trung bình của thuật toán là $O(n \log n)$, tương tự với trường hợp tốt nhất (khi mảng đã được sắp xếp).

Trong trường hợp xấu nhất, độ phức tạp là $O(n^2)$.

Trường hợp này xảy ra khi mảng được sắp xếp ngược và chọn pivot là phần tử lớn nhất/nhỏ nhất. Ví dụ, có mảng được sắp xếp giảm dần và cách chọn pivot là phần tử đầu tiên, trong khi cần sắp xếp tăng dần. Khi đó, mỗi lần chọn pivot, ta đều chọn ra phần tử lớn nhất trong mảng con, khi thực hiện partition, mảng con đó sẽ được chia thành hai mảng con có 0 và N - 1 phần tử, và khi đó, qua mỗi bước đệ quy, kích thước của mảng chỉ giảm đi được 1 phần tử. Vậy cần N bước đệ quy, mỗi bước cần duyệt toàn bộ mảng, nên độ phức tạp là $O(n^2)$.

Bubble sort

Khái niệm Bubble Sort

Ý tưởng thuật toán: So sánh các phần tử liền kề và hoán đổi vị trí của chúng nếu chúng không tuân theo thứ tự được chỉ định (tăng dần hay giảm dần).

Cách thức hoạt động:

• Bắt đầu từ chỉ số đầu tiên, ta sẽ so sánh phần tử đầu tiên và phần tử thứ hai. Nếu phần tử đầu tiên lớn hơn phần tử thứ hai, chúng sẽ được hoán đổi.

• Quá trình trên cứ tiếp tục cho đến phần tử cuối cùng.

• Sau mỗi lần lặp, phần tử lớn nhất trong số các phần tử chưa được sắp xếp sẽ được đặt ở cuối.

Mô tả thuật toán:

Tối ưu thuật toán Bubble Sort:

Trong chương trình trên, có thể có những bước so sánh thực hiện khi mảng đã được sắp xếp xong. Điều này làm tăng thời gian chạy của thuật toán.

Ta có thể tối ưu bằng cách sử dụng một biến swapped để ghi lại trạng thái đã hoán đổi hay chưa sau mỗi lần lặp. Nếu không có sự hoán đổi sau mỗi lần lặp, việc so sánh tiếp là không cần thiết.

Hàm Bubble sort

void bubbleSort(int a[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        bool swapped = false;
        for (int j = 0; j < n - 1 - i; j++)
        {
            if (a[j] > a[j + 1]) {
                swap(a[j], a[j + 1]);
                swapped = true;
            }
        }
        if (swapped == false)
            break;
    }
}

Độ phức tạp thuật toán Bubble Sort

Có hai vòng lặp được thực hiện trong thuật toán. Mỗi vòng lặp ngoài sẽ thực hiện các thao tác lặp giảm dần trong vòng lặp bên trong.

Số thao tác so sánh:

\[(n - 1) + (n - 2) + ... + 1 = \frac{n(n - 1)}{2} \approx n^2\]

Độ phức tạp thời gian trung bình và trường hợp xấu nhất của thuật toán đều là $O(n^2)$.

Trong trường hợp tốt nhất, tức là mảng đã được sắp xếp, độ phức tạp thời gian là $O(n)$.

Độ phức tạp không gian của thuật toán là $O(1)$ vì chỉ cần sử dụng một biến phụ trong thao tác hoán đổi hai phần tử. Trong trường hợp tối ưu thuật toán với biến swapped, độ phức tạp không gian của thuật toán là $O(2)$.

Shaker sort

Khái niệm Shaker sort

Ý tưởng thuật toán: Cải tiến từ Bubble sort, thay vì chỉ đi từ đầu mảng đến cuối mảng, sau mỗi lượt lặp thì phần tử lớn nhất được đưa về cuối mảng, Shaker sort đi theo cả hai chiều: chiều thuận của mảng để đưa phần tử lớn nhất về cuối mảng, chiều nghịch để đưa phần tử nhỏ nhất về đầu mảng.

Mô phỏng thuật toán:

Hàm Shaker sort

void shaker(int a[], int n)
{
    // kich thuoc mang can sap xep se giam sau moi luot lap
    // nen can thay doi gioi han mang bang bien left va right
    int left = 0, right = n - 1;
    while (left <= right)
    {
        for (int i = left; i < right; i++)
        {
            if (a[i] > a[i + 1])
                swap(a[i], a[i + 1]);
        }
        right--;

        for (int i = right; i > left; i--)
        {
            if (a[i] < a[i - 1])
                swap(a[i], a[i - 1]);
        }
        left++;
    }
}

Độ phức tạp thuật toán Shaker sort

Hoàn toàn tương tự như thuật toán Bubble sort, chỉ nhanh hơn khi phần tử lớn/nhỏ về gần đúng vị trí sớm.

Độ phức tạp thời gian trung bình và trường hợp xấu nhất của thuật toán đều là $O(n^2)$.

Trong trường hợp tốt nhất, tức là mảng đã được sắp xếp, độ phức tạp thời gian là $O(n)$.

Nhóm Insertion

Insertion sort

Khái niệm Insertion Sort

Ý tưởng thuật toán: Tương tự như việc sắp xếp các lá bài khi đánh bài. Đầu tiên, giả sử lá bài đầu tiên đã được sắp xếp, chọn một lá chưa được sắp xếp trong các lá còn lại. Nếu lá đó lớn hơn lá trên tay, nó sẽ nằm ở bên phải, ngược lại thì nằm ở bên trái.

Tổng quát, thuật toán sắp xếp chèn làm nhiệm vụ đặt một phần tử vào vị trí đúng của nó trong mỗi lần lặp.

Cách thức hoạt động của thuật toán:

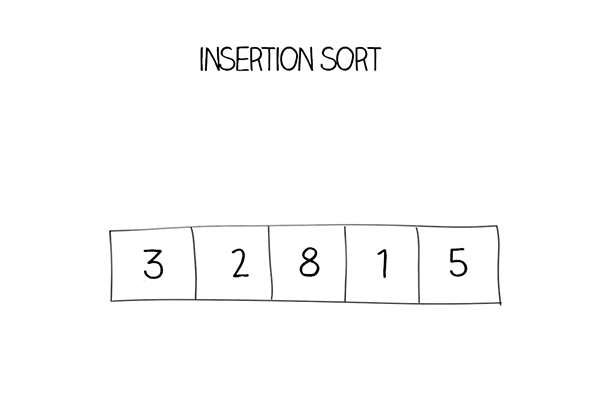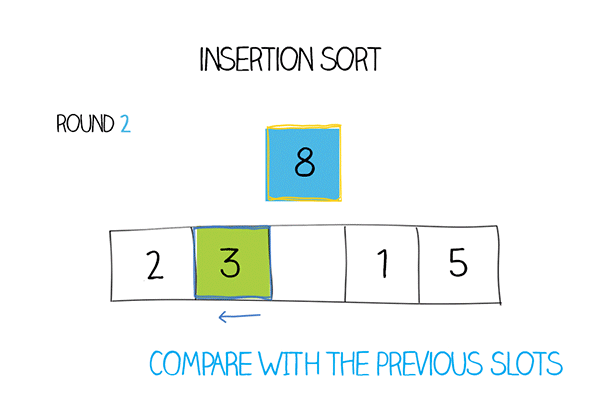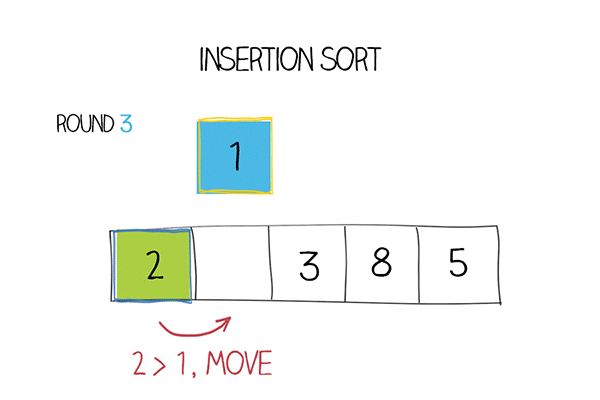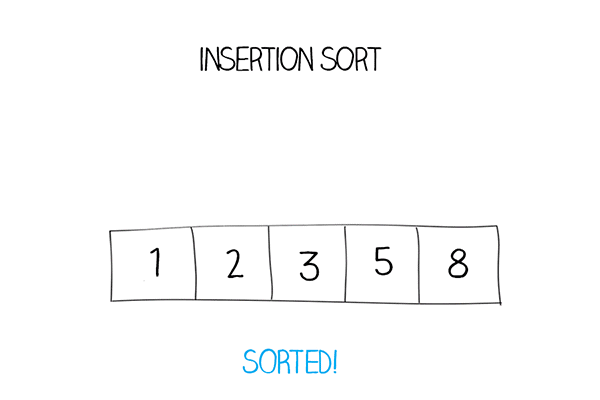
Bước 1: Phần tử đầu tiên được xem như đã được sắp xếp. Lấy phần tử thứ hai làm “khoá”, so sánh với phần tử đầu tiên, nếu “khoá” lớn hơn thì sẽ đặt ở bên phải, ngược lại thì đặt ở bên trái của phần tử đầu tiên.

Bước 2: Lúc này, hai phần tử đầu tiên xem như là đã được sắp xếp. Lấy phần tử thứ ba và so sánh với các phần tử bên trái. Từ đó, tìm được vị trí thích hợp và đặt phần tử thứ ba vào đó.

Bước 3: Lặp lại các bước trên cho đến khi mảng được sắp xếp xong.

Hàm Insertion sort

void insertion(int a[], int n)
{
    for (int i = 1; i < n; i++)
    {
        int key = a[i];
        int j = i - 1;

        while (j >= 0 && a[j] > key)
        {
            a[j + 1] = a[j];
            j--;
        }
        a[j + 1] = key;
    }
}

Độ phức tạp thuật toán Insertion Sort

Độ phức tạp không gian là $O(1)$ vì chỉ sử dụng biến phụ.

Độ phức tạp thời gian:

• Trường hợp xấu nhất: Khi có mảng được sắp xếp giảm dần từ đầu, và ta cần sắp xếp nó tăng dần. Trong trường hợp này, mỗi phần tử trong mảng với chỉ số $i$ sẽ cần thực hiện $i-1$ phép so sánh. Khi đó tổng số phép so sánh sẽ là $n*(n-1) \approx n^2$. Vậy độ phức tạp là $O(n^2)$.

• Trường hợp tốt nhất: Khi mảng đã được sắp xếp, chỉ có vòng lặp ở ngoài chạy, vòng lặp ở trong không chạy. Độ phức tạp sẽ là $O(n)$.

• Trường hợp trung bình: Khi các phần tử được sắp xếp lộn xộn, độ phức tạp là $O(n^2)$.

Binary insertion sort

Khái niệm Binary insertion sort

Ý tưởng thuật toán: Ở thuật toán Insertion sort, bước tìm kiếm vị trí thích hợp của key là một bước tìm kiếm tuyến tính (linear search) với độ phức tạp $O(n)$. Để cải tiến cho bước đó, chúng ta áp dụng binary search với độ phức tạp $O(\log n)$.

Hàm Binary insertion sort

void binary(int a[], int n)
{
    for (int i = 1; i < n; i++)
    {
        int key = a[i];
        int left = 0, right = i - 1;

        while (left <= right)
        {
            int m = (left + right) / 2;
            if (key < a[m]) right = m - 1;
            else left = m + 1;
        }
        // left la vi tri dung cua key
        for (int j = i - 1; j >= left; j--)
        {
            a[j + 1] = a[j];
        }
        a[left] = key;
    }
}

Độ phức tạp thuật toán Binary insertion sort

• Trường hợp tốt nhất: $O(n \log n)$.

• Trường hợp trung bình: $O(n^2)$.

• Trường hợp xấu nhất: $O(n^2)$.

Shell sort

Khái niệm Shell sort

Ý tưởng thuật toán: Thuật toán sắp xếp cải tiến từ Insertion sort, với mục tiêu giảm số lần hoán đổi và so sánh bằng cách sắp xếp các phần tử cách xa nhau trước, sau đó giảm khoảng cách về 1.

Cách hoạt động:

• Chia mảng thành các phần bằng nhau bằng cách chọn một giá trị khoảng cách, thường là gap hoặc interval. Ban đầu giá trị này là $\frac{n}{2}$.

• Sắp xếp các phần tử trong từng dãy con bằng cách so sánh các phần tử cách nhau gap (hoặc interval).

• Giảm khoảng cách bằng cách chia cho 2.

• Khi khoảng cách là 1 thì dừng lại.

Mô phỏng thuật toán: (Nguồn: Medium)

Hàm Shell sort

void shell(int a[], int n)
{
    for (int interval = n/2; interval > 0; interval /= 2)
    {
        for(int i = interval; i < n; i++)
        {
            int j = i;
            int value = a[i];
            for (j = i; j >= interval && a[j - interval] > value; j -= interval)
            {
                swap(a[j - interval], a[j]);
            }
        }
    }
}

Độ phức tạp thuật toán Shell sort

• Trường hợp tốt nhất: $O(n \log n)$.

• Trường hợp trung bình: $O(n \log n) \approx O(n^{1.25})$.

• Trường hợp xấu nhất: $O(n^2)$.

Nhóm Selection

Selection Sort

Khái niệm Selection Sort

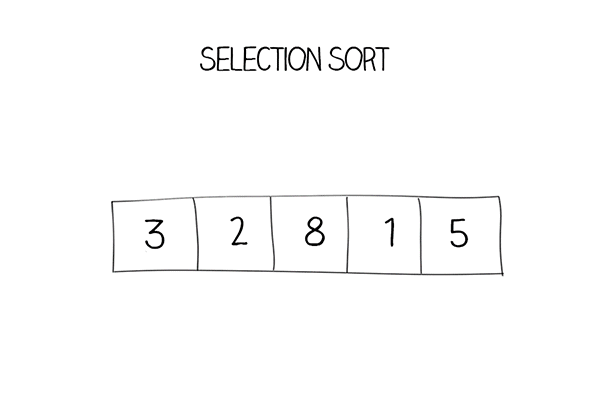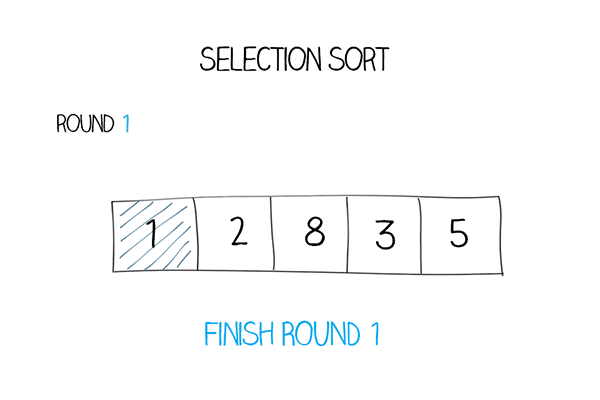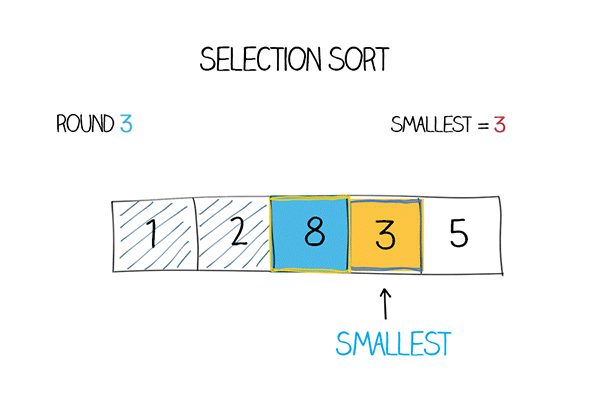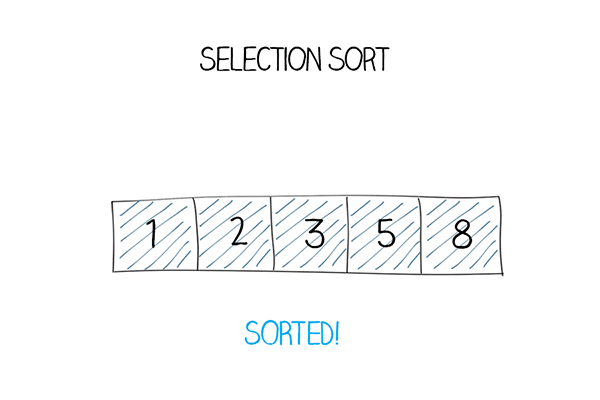
Ý tưởng thuật toán: Thuật toán Selection Sort chọn phần tử nhỏ nhất từ các phần tử chưa được sắp xếp trong mỗi lần lặp và đặt phần tử đó ở đầu mảng. Lặp liên tục cho đến khi mảng được sắp xếp.

Cách thức hoạt động:

1. Có mảng các phần tử, đặt phần tử đầu tiên làm min.

2. So sánh phần tử min đó với phần tử thứ hai, nếu nhỏ hơn min thì gán phần tử thứ hai là min.

3. Tiếp tục cho đến phần tử cuối cùng, sau khi tìm được min thật sự, hoán đổi phần tử đó với phần tử đầu tiên trong mảng.

4. Với mỗi lần lặp, chỉ số sẽ bắt đầu từ phần tử đầu tiên chưa được sắp xếp trong mảng.

Mô tả thuật toán:

Hàm Selection sort

void selection(int a[], int n)
{
    for (int i = 0; i < n - 1; i++)
    {
        int min = a[i], minIdx = i;
        for (int j = i + 1; j < n; j++)
        {
            if (a[j] < min) {
                min = a[j];
                minIdx = j;
            }
        }
        swap(a[minIdx], a[i]);
    }
}

Độ phức tạp thuật toán Selection Sort

Độ phức tạp về không gian là O(1) bởi vì chương trình chỉ sử dụng một biến trung gian để hoán đổi vị trí các phần tử.

Độ phức tạp thời gian trong tất cả các trường hợp đều là $O(n^2)$.

Heap sort

Heap là gì?

Heap là cây nhị phân đầy đủ (tức là mỗi nút có 0 hoặc 2 nút con).

Xét một nút có chỉ số $i$ (bắt đầu từ 0):

• Nút con bên trái có chỉ số $2i + 1$.

• Nút con bên trái có chỉ số $2i + 2$.

• Nút cha có chỉ số $\left\lfloor \frac{i}{2} \right\rfloor$ với $i$ lẻ, $\frac{i}{2} - 1$ với $i$ chẵn.

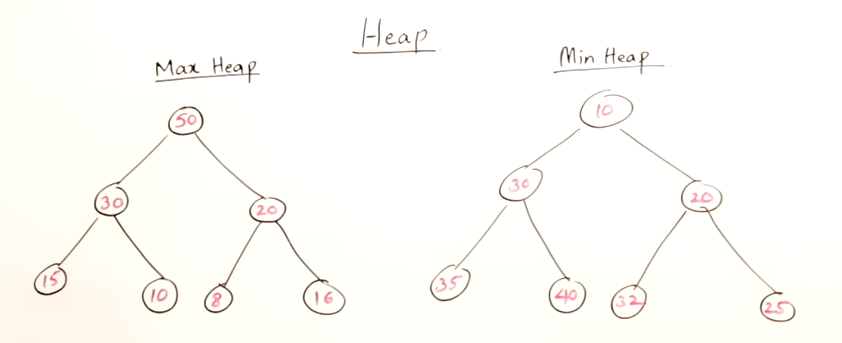
Heap có hai loại: Max Heap và Min Heap:

• Max Heap: phần tử lớn nhất nằm ở gốc, nút cha luôn lớn hơn hoặc bằng các nút con.

• Min Heap: phần tử nhỏ nhất nằm ở gốc, nút cha luôn nhỏ hơn hoặc bằng các nút con.

(Nguồn: Abdul Bari).

Thao tác Heapify

Heapify là thao tác đưa một Heap về dạng Max Heap.

Hàm Heapify làm điều đó theo hướng top-down, tức là với mỗi nút, ta thực hiện “nhìn xuống bên dưới”, nếu nó và các nút con thoả mãn là một Max Heap, ta để nguyên, ngược lại thì hoán đổi sao cho trở thành Max Heap.

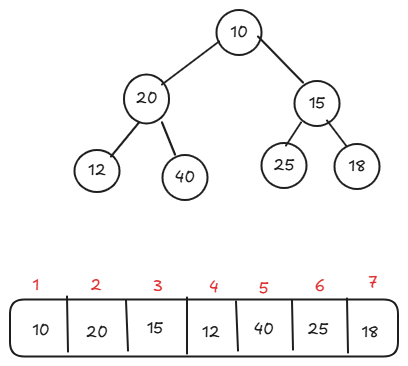
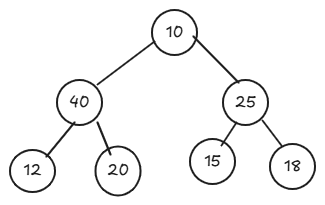
Với Heap trên, với 4 nút con 12, 40, 25, 18, nó đều thoả mãn là Max Heap.

Với nút 15, so sánh nó với các nút con 25, 18. Ta thấy nó chưa phải là Max Heap, tiến hành hoán đổi phần tử 15 với phần tử lớn hơn trong hai phần tử con. Làm tương tự với phần tử 20.

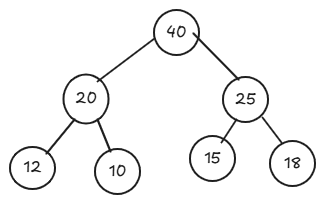
Với phần tử 10, lúc này hai phần tử con là 40 và 25, ta thực hiện hoán đổi với phần tử 40, tiếp tục thực hiện hoán đổi với phần tử 20.

Kết quả cuối cùng:

Khái niệm Heap sort

Kết hợp hai thao tác: Heapify và hoán đổi phần tử root về cuối mảng.

Sau khi nhập vào một mảng, ta bắt đầu xem nó được tổ chức dưới dạng một Heap. Nút cha cuối cùng của một Heap sẽ có chỉ số là $\frac{n}{2} - 1$.

Tiến hành Heapify từng nút cha để đảm bảo toàn bộ mảng được sắp xếp thoả mãn dưới dạng một Max Heap.

Tiếp theo, ta tiến hành hoán đổi phần tử root về cuối mảng. Sử dụng một biến chỉ số i, chạy từ cuối mảng lên đầu, kích thước của Heap cũng giảm dần theo i. Với mỗi bước hoán đổi, một phần tử lớn nhất (root) sẽ được đưa về đúng vị trí.

Sau mỗi lần hoán đổi, ta tiến hành Heapify toàn bộ Heap để đưa về dạng Max Heap.

Chương trình Heap sort

void heapify(vector<int> &a, int n, int i) //heapify a tree, root is node i
{
    int largest = i;
    // start at 0
    int l = 2 * i + 1;
    int r = 2 * i + 2;
    // if large child > root
    if (l < n && a[l] > a[largest])
        largest = l;
    // if right child > largest element
    if (r < n && a[r] > a[largest])
        largest = r;
    if (largest != i) // if root is not largest, swap
    {
        swap(a[largest], a[i]);
        //recursively heapify the next subtree
        heapify(a, n, largest);
    }
}

void heapSort(vector<int> &a)
{
    int n = a.size();

    for (int i = n/2 - 1; i >= 0; i--) // n/2 - 1 la nut cha cuoi cung
        heapify(a, n, i);
    for (int i = n - 1; i > 0; i--)
    {
        swap(a[i], a[0]);
        heapify(a, i, 0);
    }
}

Độ phức tạp thuật toán Heap sort

Trong tất cả các trường hợp, độ phức tạp đều là $O(n \log n)$.

Nhóm Merge

Merge Sort

Khái niệm Merge Sort

Ý tưởng thuật toán: Dựa trên nguyên tắc chia để trị:

• Giả sử ta cần sắp xếp mảng A. Một bài toán con sẽ là sắp xếp một phần con của mảng A bắt đầu từ chỉ số p và kết thúc ở chỉ số r, ký hiệu là A[p..r].

• Gọi q là điểm giữa p và r, ta còn có thể tách mảng con trên thành A[p..q] và A[q+1..r]. Thực hiện chia cho đến khi không thể tách được nữa.

• Khi có được hai mảng con đã sắp xếp A[p..q] và A[q+1..r] cho mảng A[p..r], ta sẽ kết hợp các kết quả bằng cách tạo một mảng đã được sắp xếp A[p..r] từ hai mảng con đã được sắp xếp ở trên.

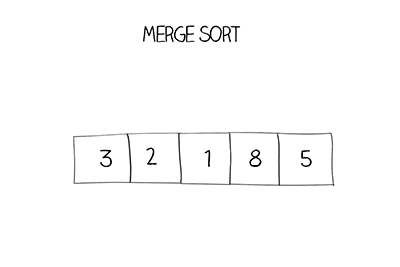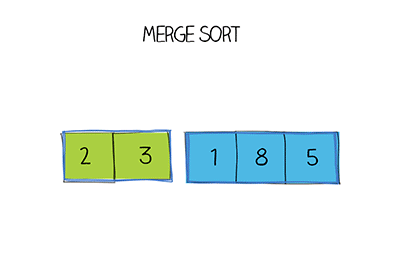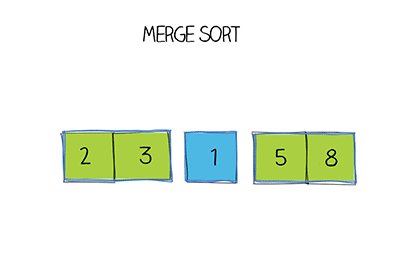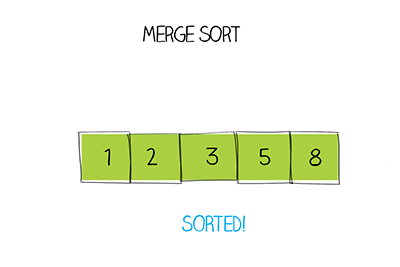
Cách thức hoạt động của thuật toán:

Hàm MergeSort sẽ chia mảng nhiều lần thành hai nửa cho đến khi kích thước mỗi mảng con là 1, khi đó p == r.

Sau đó, hàm Merge sẽ sắp xếp và kết hợp các mảng con thành mảng lớn hơn.

Pseudo code:

Hàm MergeSort với các tham số là (A, p, r):
    Nếu p > r
        Kết thúc hàm và trả về
    q = (p+r)/2
    MergeSort(A, p, q)
    MergeSort(A, q+1, r)
    Merge(A, p, q, r)

Để sắp xếp toàn bộ mảng, đầu tiên cần gọi hàm MergeSort(A, 0, length(A) - 1).

Bước quan trọng nhất là bước trộn trong hàm Merge. Trong hàm này sử dụng kĩ thuật hai con trỏ để vừa so sánh vừa hợp nhất mảng.

Pseudo code:

Chúng ta đã đi đến phần cuối của bất kỳ mảng nào hay chưa?
     Nếu chưa:
         Thực hiện so sánh các phần tử hiện tại của cả hai mảng
         Sao chép phần tử nhỏ hơn vào mảng đã sắp xếp
         Di chuyển con trỏ của phần tử có chứa phần tử nhỏ hơn
     Nếu có:
         Sao chép tất cả các phần tử còn lại của mảng không rỗng.

Hàm Merge sort

void merge(int a[], int l, int m, int r)
{
    int n = r - l + 1;  // kich thuoc mang sau khi gop
    int t[n];           // mang sau khi gop
    int p1 = l;         // con tro den mang con 1
    int p2 = m + 1;     // con tro den mang con 2
    int k = 0;          // con tro den mang ket qua

    while (p1 <= m && p2 <= r)
    {
        if (a[p1] <= a[p2])
            t[k++] = a[p1++];
        else
            t[k++] = a[p2++];
    }

    while (p1 <= m)
        t[k++] = a[p1++];
    while (p2 <= r)
        t[k++] = a[p2++];

    for (int i = l; i <= r; i++)
    {
        a[i] = t[i - l]; //dua mang t vao mang a
    }
}

void mergeSort(int a[], int l, int r)
{
    if (l >= r)
        return;
    int m = (l + r) / 2;
    mergeSort(a, l, m);
    mergeSort(a, m + 1, r);
    merge(a, l, m, r);
}

Độ phức tạp thuật toán Merge Sort

Trong thuật toán Merge Sort, mảng được chia hai liên tục cho đến khi mảng con có kích thước là 1. Khi đó, số lần chia hai mảng sẽ là $\log_{2}n$.

Tương ứng với mỗi bước chia đôi mảng là một bước gộp hai mảng con. Ở mỗi bước đệ quy để gộp mảng, hàm Merge thực hiện $n$ bước đặt phần tử vào mảng. Do đó, độ phức tạp thời gian của thao tác này là $O(n)$.

Tổng lại, độ phức tạp của thuật toán là $O(n \log n)$.

Độ phức tạp trên đúng với cả ba trường hợp tốt nhất, xấu nhất hay trung bình.

Nhóm Specific

Counting sort

Khái niệm Counting sort

Counting sort là một thuật toán sắp xếp không so sánh (non-comparison-based).

Ý tưởng thuật toán: Sử dụng một mảng đếm, tạm gọi là f, để lưu vị trí cuối cùng của một phần tử ở trong mảng sau khi sắp xếp.

Cách hoạt động của thuật toán: Đầu tiên, ta duyệt qua mảng f để lưu tần suất của các phần tử riêng biệt trong mảng, thao tác này đơn giản với phép toán: f[a[i]]++ (f[i] lưu tần suất của giá trị i).

Sau đó, duyệt qua một lần nữa và thực hiện phép toán: f[i] += f[i - 1]. Lúc này, giá trị của f[i] sẽ là số phần tử bé hơn hoặc bằng phần tử có giá trị i trong mảng. Khi đó, f[i] cũng chính là vị trí xuất hiện cuối cùng của phần tử có giá trị i trong mảng sau khi sắp xếp.

Hàm Counting sort

void counting(int a[], int n)
{
    int m = a[0];
    for (int i = 1; i < n; i++)
        m = max(m, a[i]);
    // m la max cua mang a
    // range cua mang la [0, m]

    int f[m + 1] = {0};

    for (int i = 0; i < n; i++)
        f[a[i]]++; // f[i] luu tan suat cua phan tu co gia tri i trong mang a

    for (int i = 1; i <= m; i++)
        f[i] += f[i - 1]; // f[i] luu so luong phan tu trong mang a <= i
    // f[i] chinh la chi so cua phan tu cuoi cung co gia tri i trong mang sau khi sap xep.

    int b[n];
    for (int i = n - 1; i >= 0; i--)
    {
        b[f[a[i]] - 1] = a[i];
        f[a[i]]--;
    }
    for (int i = 0; i < n; i++)
        a[i] = b[i];
}

Độ phức tạp thuật toán Counting sort

Ta có N là kích thước của mảng nhập vào, M là kích thước của mảng đếm (cũng là giá trị lớn nhất, hay giới hạn trên của khoảng giá trị của mảng).

Độ phức tạp thuật toán: $O(N + M)$ trong tất cả các trường hợp.

Radix sort

Khái niệm Radix sort

Ý tưởng thuật toán: Sắp xếp dựa trên hệ số của các chữ số (least significant digit → most significant digit).

Mô phỏng thuật toán:

Giả sử ta có mảng: [28, 143, 550, 7, 911, 220].

Số lớn nhất trong dãy có 3 chữ số → cần 3 lần sắp xếp lại mảng để thu được mảng chính xác.

Ta tạo ra một mảng hai chiều bin, gồm 10 dòng ứng với 10 chữ số từ 0 đến 9. Với mỗi dòng, lưu các số có chữ số đang xét tương ứng.

Ví dụ:

Đầu tiên, ta xét cơ số là 1, tức chữ số hàng đơn vị. Sắp xếp các số vào dãy bin như sau:

Mảng trở thành: [550, 220, 911, 143, 7, 28], tức là đã được sắp xếp theo thứ tự tăng dần của chữ số hàng đơn vị.

Tiếp theo, cơ số trở thành 10:

Mảng trở thành: [7, 911, 220, 28, 143, 550], tức là đã được sắp xếp theo thứ tự tăng dần của chữ số hàng chục, nếu chữ số hàng chục bằng nhau thì sắp xếp tăng dần theo chữ số hàng đơn vị.

Tiếp theo, cơ số trở thành 100 (cuối cùng, vì số lớn nhất có 3 chữ số):

Mảng đã được sắp xếp.

Hàm Radix sort

void radix(vector<int> &a)
{
    int n = a.size();

    int maxValue = *max_element(a.begin(), a.end());

    vector<vector<int>> bins(10, vector<int>(n));
    vector<int> counts(10);

    for (int exp = 1; maxValue/exp > 0; exp *= 10)
    {
        //reset counts
        fill(counts.begin(), counts.end(), 0);
        // voi moi a[i], lay ra chu so ung voi exp tuong ung, dua so do vao bins
        for (int i = 0; i < n; i++)
        {
            int digit = (a[i] / exp) % 10;
            bins[digit][count[digit]] = a[i];
            count[digit]++;
        }
        // tao lai mang a de dung cho exp tiep theo
        int index = 0;
        for (int i = 0; i < 10; i++)
        {
            for (int j = 0; j < counts[i]; j++)
            {
                a[index] = bins[i][j];
                index++;
            }
        }
    }
}

Độ phức tạp thuật toán Radix sort

Thuật toán có độ phức tạp thời gian trong mọi trường hợp là $O(dn)$, với $d$ là số chữ số của số lớn nhất trong mảng, $n$ là số lượng phần tử của mảng.