[CryptoHack] Elliptic Curves

Background Reading

Elliptic Curve Cryptography (ECC) is an asymmetric cryptography protocol that, like RSA and Diffie-Hellman, relies on a trapdoor function (which is easy to compute in one direction but hard to reverse without a secret).

For RSA, the trapdoor function is based on the difficulty of factoring large numbers. For Diffie-Hellman, the trapdoor function is based on the difficulty of the Discrete Logarithm Problem in a finite field. For ECC, the trapdoor function is based on the difficulty of the Elliptic Curve Discrete Logarithm Problem.

Let's start with the definition of an elliptic curve. An elliptic curve is based on the equation of the form:

$$Y^2 = X^3 + aX + b$$

This equation is called Weierstrass equation. For example, this is the graph of the elliptic curve defined by the equation $Y^2 = X^3 - 2X + 4$:

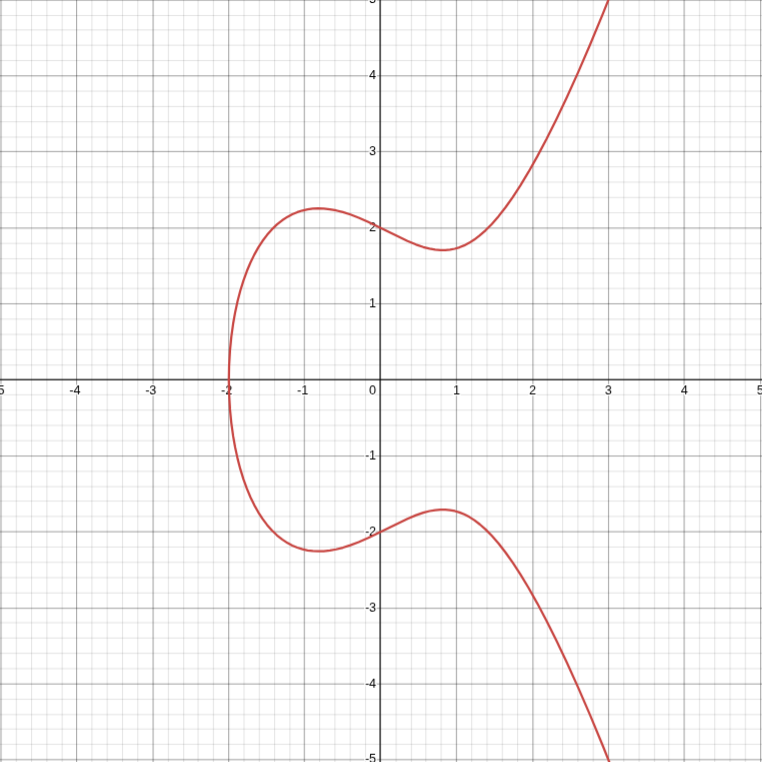
Elliptic curves have an amazing property: given two points on the curve, you can "add" them together to get a third point on the curve.

So, what makes the difficulty of ECC? We can understand the scalar multiplication of a point as the repeated addition of that point to itself. For example, $Q = [2]P = P + P$.

It turns out that scalar multiplication is a trapdoor function: It's easy to compute $Q$ from given $P$ but hard to finding $n$ such that $Q = [n]P$, given $P$ and $Q$.

This addition operation is defined geometrically: if you draw a line through two points on the curve, it will intersect the curve at a third point. Reflecting this point across the x-axis gives you the result of the addition.

How do we understand point addition?

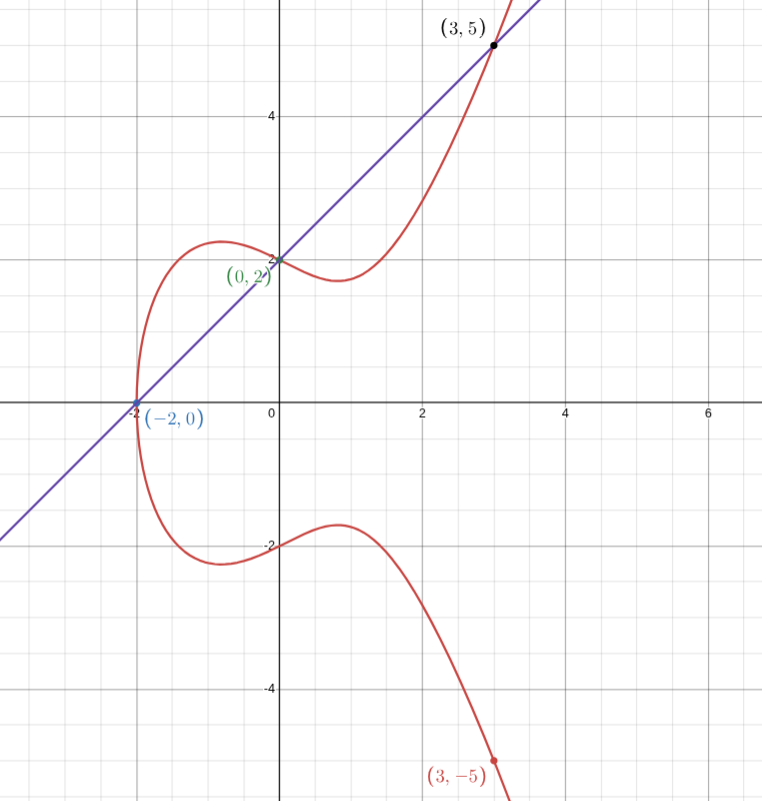
Take an elliptic curve and mark the two points $P$, $Q$ along the curve with their coordinates. Draw a straight line through both points, and find the third point where the line intersects the curve. Reflect this point across the x-axis to get the result of $P + Q$.

For example, take the curve above $Y^2 = X^3 - 2X + 4$ and two points $P = (-2, 0)$ and $Q = (0, 2)$. The line $y = x + 2$ passes through both points, and intersects the curve at the third point $R = (3, 5)$. Reflecting $R$ across the x-axis gives us the result of the addition: $R' = (3, -5)$

Looking at other cases of point addition:

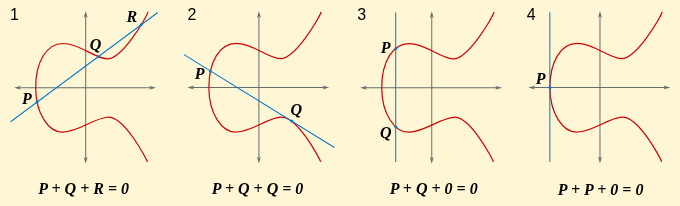
Source: CryptoHack.

The second graph shows the case where the line is tangent to the curve at point $Q$. We define that the line intersects Q twice, so the equation is: $P + Q + Q = 0$.

The third graph shows the case where $P$ and $Q$ are vertically aligned. In this case, the line intersects the curve at the point at infinity, which we denote as $O$. We define that $P + Q + O = 0$.

The last graph shows the case where $P = Q$. Because the line is tangent to the point, it is defined to be intersected twice, at the third point is $0$. So, we have $P + P + O = 0$.

In conclusion, an elliptic curve $E$ is the set of solutions for the Weierstrass equation, together with a point at infinity $O$.

The constants $a$ and $b$ must satisfy the condition: $4a^3 + 27b^2 \neq 0$ to ensure that the curve is non-singular. It means the curve must be totally smooth, does not have any cusps or self-intersections.

Let $E$ be an elliptic curve, point addition has some properties:

$$P + O = O + P = P \\ P + (-P) = O \\ (P + Q) + R = P + (Q + R) \\ P + Q = Q + P$$

In ECC, we study elliptic curves over a finite field $F_p$, where $p$ is a prime number. This means an elliptic curve is no longer a continuous curve but a set of discrete points with integer coordinates modulo $p$.

Point negation

To apply ellictic curve in cryptography, we need to study curves over finite fields $F_p$. It is no longer a geometric curve but a set of discrete points with integer coordinates modulo $p$.

$$E(F_p) = \{(x, y): x, y \in F_p \space \text{satisfying} \space y^2 = x^3 + ax + b \mod p \} \cup \{O\}$$

For example, consider the curve:

$$E: Y^2 = X^3 + 497X + 1768 \mod 9739$$

Using the above curve and the point $P = (8045, 6936)$, find the point $Q(x, y)$ such that $Q = -P$.

Solution:

To find the point $Q = -P$, we need to negate the y-coordinate of point $P$. The negation of a point on an elliptic curve is defined as reflecting the point across the x-axis.

Given point $P = (8045, 6936)$, the negation of the y-coordinate is calculated as follows:

$$Q = (x_P, -y_P)$$

But in a finite field $F_p$, we need to compute the negation modulo $p$:

$$-y_P \equiv p - y_P \mod p$$

Apply to our case:

$$x_Q = x_P = 8045$$ $$y_Q \equiv 9739 - 6936 \mod 9739 \rightarrow y_Q \equiv 2803 \mod 9739$$

Thus, the point $Q$ is:

$$Q (8045, 2803)$$

Point Addition

The following algorithm describes how to add two points $P$ and $Q$ on an elliptic curve over a finite field $F_p$.

Algorithm for the addition of two points P and Q:

(1) If $P = O$, then $P + Q = Q$, return $Q$.

(2) If $Q = O$, then $P + Q = P$, return $P$.

(3) Otherwise, write $P = (x_1, y_1)$ and $Q = (x_2, y_2)$.

(4) If $x_1 \equiv x_2 \mod p$ and $y_1 \equiv -y_2 \mod p$, then $P + Q = O$, return $O$.

(5) Otherwise:

If $P \neq Q$, $m \equiv (y_2 - y_1)(x_2 - x_1)^{-1} \mod p$

Else (if $P = Q$), $m \equiv (3x_1^2 + a)(2y_1)^{-1} \mod p$

with $m$ is the slope of the line through points $P$ and $Q$.

(6) $x_3 \equiv m^2 - x_1 - x_2 \mod p$

(7) $y_3 \equiv m(x_1 - x_3) - y_1 \mod p$

(8) Return the point $R = (x_3, y_3)$.

Note: We are working with a finite field, so the above calculations should be done modulo $p$, and we do not divide directly; instead, we multiply by the modular inverse.

For example, consider the elliptic curve:

$$Y^2 = X^3 + 497X + 1768 \mod 9739$$

Using the above curve and the points $P = (493, 5564)$, $Q = (1539, 4742)$, $R = (4403, 5202)$, find the point $S$ such that $S = P + P + Q + R$ by implementing the above algorithm.

Solution:

from Crypto.Util.number import inverse
a = 497
b = 1768
p = 9739

P = (493, 5564)
Q = (1539, 4742)
R = (4403, 5202)

def addPoints(P, Q):
    if P == (0, 0):
        return Q
    if Q == (0, 0):
        return P
    
    (x1, y1) = P
    (x2, y2) = Q
    
    if (x1 == x2) and (y1 == p - y2):
        return (0, 0)
    
    if (x1, y1) == (x2, y2):
        t1 = 3 * x1 * x1 + a
        t2 = 2 * y1
    else:
        t1 = y2 - y1
        t2 = x2 - x1
    
    inv = inverse(t2, p)
    m = (t1 * inv) % p
    
    x3 = (m * m - x1 - x2) % p
    y3 = (m * (x1 - x3) - y1) % p
    return (x3, y3)

P2 = addPoints(P, P)
P2_Q = addPoints(P2, Q)
S = addPoints(P2_Q, R)
print(f"S = {S}")

Running the above code will give the result:

S = (4215, 2162)

Scalar Multiplication

Scalar multiplication is the process of adding a point $P$ to itself repeatedly to obtain another point $Q = [n]P$. For example, $[3]P = P + P + P$.

Scalar multiplication is used to generate a shared secret over an insecure channel, similar to the Diffie-Hellman key exchange.

The below algorithm describes how to perform scalar multiplication of a point on an elliptic curve.

Double and Add algorithm for the scalar multiplication:

Input: $P \in E(F_p)$, an integer $n > 0$.

Output: $Q = [n]P \in E(F_p)$

(1): Set $Q = P$ and $R = O$.

(2): Loop while $n > 0$:

(3): If $n \equiv 1 \mod 2$, set $R = R + Q$.

(4): Set $Q = Q + Q$ and $n = n // 2$.

(5): If $n > 0$, go to step (2).

(6): Return $R$, which is equal to $[n]P$.

For example, consider the elliptic curve:

$$Y^2 = X^3 + 497X + 1768 \mod 9739$$

Using the above curve and the point $P = (2339, 2213)$, find the point $Q(x, y)$ such that $Q = [7863]P$ by implementing the above algorithm.

Solution:

from Crypto.Util.number import inverse

a = 497
b = 1768
p = 9739
P = (2339, 2213)

def scalarMultiply(n, P):
    if n <= 0:
        return (0, 0)
    Q = P
    R = (0, 0)
    while n > 0:
        if n % 2 == 1:
            R = addPoints(R, Q)
        Q = addPoints(Q, Q)
        n = n // 2
    return R

n = 7863
nP = scalarMultiply(n, P)
print(f"nP = {nP}")

Running the above code will give the result:

nP = (9467, 2742)

Curves and Logs

The Elliptic Curve Discrete Logarithm Problem (ECDLP) is the problem of finding an integer $n$ such that $Q = [n]P$, given points $P$ and $Q$ on an elliptic curve. This is a trapdoor function, as it is easy to compute $Q$ from $P$ and $n$, but hard to find $n$ given $P$ and $Q$.

Alice and Bob are talking and they want to create a shared secret so they can start encrypting their messages with some symmetric cryptographic protocol Alice and Bob don't trust their connection, so they need a way to create a secret others can't replicate.

Alice and Bob agree on an elliptic curve $E$ over a finite field $F_p$, a prime $p$ and a generator point $G$ on the curve which generates a subgroup $H = \langle G \rangle$ of large prime order $q$.

In ECC, it's important that the order of the subgroup generated by the base point $G$ is a large prime number.

The Elliptic Curve Diffle-Hellman key exchange happens as follows:

• Alice generates a secret random integer $n_a$ and calculates her public key $Q_a = [n_a]G$. She sends $Q_a$ to Bob.

• Bob generates a secret random integer $n_b$ and calculates his public key $Q_b = [n_b]G$. He sends $Q_b$ to Alice.

• Due to the difficulty of ECDLP, an man-in-the-middle attacker cannot compute the shared secret.

• Then, Alice calculates the shared secret $S = [n_a]Q_b$, and Bob's shared secret is $S = [n_b]Q_a$.

• Due to the properties of point multiplication, both shared secrets are equal: $S = [n_a][n_b]G = [n_b][n_a]G$.

• Alice and Bob can now use the shared secret $S$ to derive a symmetric key for encrypting their messages.

Challenge: Using the curve, prime and generator below, calculate the shared secret after Alice sends Bob $Q_a = (815, 3190)$, with Bob's secret integer is $n_b = 1829$.

$$E: Y^2 = X^3 + 497X + 1768 \mod 9739, \space G = (1804, 5368)$$

Generate a key by calculating the SHA1 hash of the $x$ coordinate (take the integer and cast it to string), the flag is the hexdigest.

n = 1829
Q_A = (815, 3190)
S = scalarMultiply(n, Q_A)
x_coord = S[0]

import hashlib
hash = hashlib.sha1()
hash.update(str(x_coord).encode())
print(f"sha1(S) = {hash.hexdigest()}")

Efficient Exchange

Challenge: This time, Alice and Bob want to try and keep their data transfer as efficient as possible and realise that sending both $x$ and $y$ coordinates of their public keys is a bit wasteful. They decide to just send the $x$ coordinate.

As long as Alice and Bob agree on the curve parameters, there are only ever two possible values of $y$ for a given $x$. In fact, given either of the values of $y$, the shared secret will have the same $x$ coordinate.

Using the curves:

$$E: Y^2 = X^3 + 497X + 1768 \mod 9739, \space G = (1804, 5368)$$

Calculate the shared secret after Alice sends Bob only $x = 4726$, and Bob's secret integer is $n_b = 6534$. Using the $x$ coordinate to decrypt the flag.

{
    'iv': 'cd9da9f1c60925922377ea952afc212c', 
    'encrypted_flag': 'febcbe3a3414a730b125931dccf912d2239f3e969c4334d95ed0ec86f6449ad8'
}

In this challenge, we only have $x$, so we need to calculate $y$ from $x$ using the curve equation. Obviously, we will have $y^2$ by put $x$ into the curve equation. Moreover, $p = 9739 \equiv 3 \mod 4$, so we can calculate $y$ by:

$$y = \pm \sqrt{y^2} = \pm (y^2)^{\frac{p+1}{4}} \mod p$$

Solution:

nb = 6534
x_QA = 4726

y_2 = (x_QA * x_QA * x_QA + a * x_QA + b) % p
y_QA = pow(y_2, (p + 1) // 4, p)
Q_A = (x_QA, y_QA)
S = scalarMultiply(nb, Q_A)
print(f"S = {S}")

Montgomery's Ladder

We have used the double-and-add algorithm for scalar multiplication, but it has a vulnerability to side-channel attacks. Because this algorithm does not always perform calculations, so the time between each step will have variations, an attacker can monitor the time taken for each operation and deduce information about the secret integer $n$ based on whether a point addition or doubling was performed.

To mitigate this vulnerability, we can use Montgomery's Ladder algorithm for scalar multiplication. This algorithm ensures that both point addition and point doubling are performed in each iteration, making it resistant to side-channel attacks.

Montgomery’s binary algorithm:

Input: $P \in E(F_p)$ and an $n$-bit integer $k = \sum{2^i k_i}$ where $k_{n-1} = 1$.

Output: $Q = [k]P \in E(F_p)$

(1): Set $(R_0, R_1)$ to $(P, [2]P)$

(2): For $i$ from $n-2$ down to $0$:

(3): If $k_i = 0$

(4): Set $(R_0, R_1) = ([2]R_0, R_0 + R_1)$

(5): Else

(6): Set $(R_0, R_1) = (R_0 + R_1, [2]R_1)$

(7): Return $R_0$, which is equal to $[k]P$.

This algorithm ensures that both point addition and point doubling are performed in each iteration, making it resistant to side-channel attacks.

Challenge: Consider the following curve:

$$E: Y^2 = X^3 + 486662X^2 + X \mod 2^{255} - 19$$

Using the above curve and the generator point $G$ with $G.x = 9$, find the coordinate $x_Q$ of the point $Q = [0x1337c0decafe]G$, using the Montgomery's Ladder algorithm.

The curve above is in Montgomery form, the general equation is:

$$E: BY^2 = X^3 + AX^2 + X$$

Addition formular for Montgomery Curve (Affine):

Input: $P, Q \in E(F_p)$ with $P \neq Q$.

Output: $R = P + Q \in E(F_p)$

$(x1, y1), (x2, y2) = P, Q$ $\alpha = (y2 - y1)/(x2 - x1) \mod p$ $x_3 = B\alpha^2 - A - x1 - x2 \mod p$ $y_3 = \alpha(x1 - x3) - y1 \mod p$ $R = (x_3, y_3)$

Doubling formular for Montgomery Curve (Affine):

Input: $P, Q \in E(F_p)$ with $P \neq Q$.

Output: $R = [2]P \in E(F_p)$

$(x_1, y_1) = P$ $\alpha = (3x_1^2 + 2Ax_1 + 1)/(2By_1) \mod p$ $x_3 = B\alpha^2 - A - 2x_1 \mod p$ $y_3 = \alpha(x_1 - x_3) - y_1 \mod p$ $R = (x_3, y_3)$

Solution:

P = 2**255 - 19
A = 486662
B = 1

G_X = 9
K_HEX = "0x1337c0decafe"
K = int(K_HEX, 16)

def mod_inverse(n, p):
    return pow(n, p - 2, p)

def modular_sqrt(a, p):
    v = pow(2 * a, (p - 5) // 8, p)
    i = (2 * a * v * v) % p
    x = (a * v * (i - 1)) % p
    if (x * x) % p == a:
        return x
    return None

def point_add(P1, P2):
    x1, y1 = P1
    x2, y2 = P2
    if x1 == x2: return point_double(P1)
    alpha = ((y2 - y1) * mod_inverse(x2 - x1, P)) % P
    x3 = (B * pow(alpha, 2, P) - A - x1 - x2) % P
    y3 = (alpha * (x1 - x3) - y1) % P 
    return (x3, y3)

def point_double(P1):
    x1, y1 = P1
    num = (3 * pow(x1, 2, P) + 2 * A * x1 + 1) % P
    den = (2 * B * y1) % P
    alpha = (num * mod_inverse(den, P)) % P
    x3 = (B * pow(alpha, 2, P) - A - 2 * x1) % P
    y3 = (alpha * (x1 - x3) - y1) % P
    return (x3, y3)

def montgomery_ladder(P_point, k):
    r0 = P_point
    r1 = point_double(P_point)
    bits = bin(k)[3:] 
    for bit in bits:
        if bit == '0':
            r1 = point_add(r0, r1)
            r0 = point_double(r0)
        else:
            r0 = point_add(r0, r1)
            r1 = point_double(r1)
    return r0

rhs = (pow(G_X, 3, P) + A * pow(G_X, 2, P) + G_X) % P
G_Y = modular_sqrt(rhs, P)
G = (G_X, G_Y)

Q = montgomery_ladder(G, K)

print(Q[0])

Smooth Criminal

Challenge: Spent my morning reading up on ECC and now I'm ready to start encrypting my messages. Sent a flag to Bob today, but you'll never read it.

Challenge files:

source.py:

from Crypto.Cipher import AES
from Crypto.Util.number import inverse
from Crypto.Util.Padding import pad, unpad
from collections import namedtuple
from random import randint
import hashlib
import os

Point = namedtuple("Point", "x y")

O = 'Origin'

FLAG = b'crypto{??????????????????????????????}'


def check_point(P: tuple):
    if P == O:
        return True
    else:
        return (P.y**2 - (P.x**3 + a*P.x + b)) % p == 0 and 0 <= P.x < p and 0 <= P.y < p


def point_inverse(P: tuple):
    if P == O:
        return P
    return Point(P.x, -P.y % p)


def point_addition(P: tuple, Q: tuple):
    # based of algo. in ICM
    if P == O:
        return Q
    elif Q == O:
        return P
    elif Q == point_inverse(P):
        return O
    else:
        if P == Q:
            lam = (3*P.x**2 + a)*inverse(2*P.y, p)
            lam %= p
        else:
            lam = (Q.y - P.y) * inverse((Q.x - P.x), p)
            lam %= p
    Rx = (lam**2 - P.x - Q.x) % p
    Ry = (lam*(P.x - Rx) - P.y) % p
    R = Point(Rx, Ry)
    assert check_point(R)
    return R


def double_and_add(P: tuple, n: int):
    # based of algo. in ICM
    Q = P
    R = O
    while n > 0:
        if n % 2 == 1:
            R = point_addition(R, Q)
        Q = point_addition(Q, Q)
        n = n // 2
    assert check_point(R)
    return R


def gen_shared_secret(Q: tuple, n: int):
    # Bob's Public key, my secret int
    S = double_and_add(Q, n)
    return S.x


def encrypt_flag(shared_secret: int):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Encrypt flag
    iv = os.urandom(16)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ciphertext = cipher.encrypt(pad(FLAG, 16))
    # Prepare data to send
    data = {}
    data['iv'] = iv.hex()
    data['encrypted_flag'] = ciphertext.hex()
    return data


p = 310717010502520989590157367261876774703
a = 2
b = 3

g_x = 179210853392303317793440285562762725654
g_y = 105268671499942631758568591033409611165
G = Point(g_x, g_y)

n = randint(1, p)

public = double_and_add(G, n)
print(public)

b_x = 272640099140026426377756188075937988094
b_y = 51062462309521034358726608268084433317
B = Point(b_x, b_y)

shared_secret = gen_shared_secret(B, n)

ciphertext = encrypt_flag(shared_secret)
print(ciphertext)

Output:

Point(x=280810182131414898730378982766101210916, y=291506490768054478159835604632710368904)

{'iv': '07e2628b590095a5e332d397b8a59aa7', 'encrypted_flag': '8220b7c47b36777a737f5ef9caa2814cf20c1c1ef496ec21a9b4833da24a008d0870d3ac3a6ad80065c138a2ed6136af'}

The curve given:

$E: Y^2 = X^3 + 2X + 3 \mod 310717010502520989590157367261876774703$

To calculate the shared secret, we have to find $n$, then based on Bob's public key $B$ to calculate $S = [n]B$. In this case, $p$ is a large prime number, so we cannot brute-force $n$. Using SageMath to solve discrete log problem:

p = 310717010502520989590157367261876774703
a = 2
b = 3
E = EllipticCurve(GF(p), [a, b])

G = E(179210853392303317793440285562762725654, 105268671499942631758568591033409611165)
PA = E(280810182131414898730378982766101210916, 291506490768054478159835604632710368904)

n = G.discrete_log(PA)
print(f"Secret n found: {n}")

bx = 272640099140026426377756188075937988094
by = 51062462309521034358726608268084433317
B = E(bx, by)
S = n * B
print(f"Shared Secret x: {S[0]}")

After getting the shared secret $S.x$, we can derive the AES key and decrypt the flag:

from Crypto.Cipher import AES
import hashlib

shared_secret = '171172176587165701252669133307091694084'
iv = bytes.fromhex('07e2628b590095a5e332d397b8a59aa7')
encrypted_flag = bytes.fromhex('8220b7c47b36777a737f5ef9caa2814cf20c1c1ef496ec21a9b4833da24a008d0870d3ac3a6ad80065c138a2ed6136af')

sha1 = hashlib.sha1()
sha1.update(str(shared_secret).encode('ascii'))
key = sha1.digest()[:16]

cipher = AES.new(key, AES.MODE_CBC, iv)
flag = cipher.decrypt(encrypted_flag)
print(flag)

Curveball

Challenge: Here's my secure search engine, which will only search for hosts it has in its trusted certificate cache.

Challenge files:

#!/usr/bin/env python3

import fastecdsa
from fastecdsa.point import Point
from fastecdsa.curve import P256
from utils import listener


FLAG = "crypto{????????????????????????????????????}"
G = P256.G
assert G.x, G.y == [0x6B17D1F2E12C4247F8BCE6E563A440F277037D812DEB33A0F4A13945D898C296,
                    0x4FE342E2FE1A7F9B8EE7EB4A7C0F9E162BCE33576B315ECECBB6406837BF51F5]


class Challenge():
    def __init__(self):
        self.before_input = "Welcome to my secure search engine backed by trusted certificate library!\n"
        self.trusted_certs = {
            'www.cryptohack.org': {
                "public_key": Point(0xE9E4EBA2737E19663E993CF62DFBA4AF71C703ACA0A01CB003845178A51B859D, 0x179DF068FC5C380641DB2661121E568BB24BF13DE8A8968EF3D98CCF84DAF4A9, curve=P256),
                "curve": "secp256r1",
                "generator": [G.x, G.y]
            },
            'www.bing.com': {
                "public_key": Point(0x3B827FF5E8EA151E6E51F8D0ABF08D90F571914A595891F9998A5BD49DFA3531, 0xAB61705C502CA0F7AA127DEC096B2BBDC9BD3B4281808B3740C320810888592A, curve=P256),
                "curve": "secp256r1",
                "generator": [G.x, G.y]
            },
            'www.gchq.gov.uk': {
                "public_key": Point(0xDEDFC883FEEA09DE903ECCB03C756B382B2302FFA296B03E23EEDF94B9F5AF94, 0x15CEBDD07F7584DBC7B3F4DEBBA0C13ECD2D2D8B750CBF97438AF7357CEA953D, curve=P256),
                "curve": "secp256r1",
                "generator": [G.x, G.y]
            }
        }

    def search_trusted(self, Q):
        for host, cert in self.trusted_certs.items():
            if Q == cert['public_key']:
                return True, host
        return False, None

    def sign_point(self, g, d):
        return g * d

    def connection_host(self, packet):
        d = packet['private_key']
        if abs(d) == 1:
            return "Private key is insecure, certificate rejected."
        packet_host = packet['host']
        curve = packet['curve']
        x, y = packet['generator']
        g = Point(x, y, curve=P256)
        Q = self.sign_point(g, d)
        cached, host = self.search_trusted(Q)
        if cached:
            return host
        else:
            self.trusted_certs[packet_host] = {
                "public_key": Q,
                "curve": "secp256r1",
                "generator": G
            }
            return "Site added to trusted connections"

    def bing_it(self, s):
        return f"Hey bing! Tell me about {s}"

    #
    # This challenge function is called on your input, which must be JSON
    # encoded
    #
    def challenge(self, your_input):
        host = self.connection_host(your_input)
        if host == "www.bing.com":
            return self.bing_it(FLAG)
        else:
            return self.bing_it(host)


import builtins; builtins.Challenge = Challenge # hack to enable challenge to be run locally, see https://cryptohack.org/faq/#listener
listener.start_server(port=13382)

Explain the challenge: The server will return the flag only if it recognizes the host as www.bing.com. To do this, we need to create a certificate that matches the public key of www.bing.com. From the source code, we can see that the server allows us to enter any private key d and generator point G. The public key is calculated as Q = [d]G.

To forge a certificate for www.bing.com, we need to find a private key d and a generator point G such that the resulting public key Q matches the public key of www.bing.com.

Solution: We can choose d = 2 (to avoid the condition abs(d) == 1) and calculate the generator point G as:

$$G = [d^{-1}]Q_{bing} = [2^{-1}]Q_{bing}$$

Using the fastecdsa library, we can implement this as follows:

from fastecdsa.point import Point
from fastecdsa.curve import P256
import json

bing_pub_x = 0x3B827FF5E8EA151E6E51F8D0ABF08D90F571914A595891F9998A5BD49DFA3531
bing_pub_y = 0xAB61705C502CA0F7AA127DEC096B2BBDC9BD3B4281808B3740C320810888592A
Q_bing = Point(bing_pub_x, bing_pub_y, curve=P256)

d = 2

n = P256.q
d_inv = pow(d, -1, n)
g = Q_bing * d_inv

payload = {
    "private_key": d,
    "host": "attacker.com",
    "curve": "secp256r1",
    "generator": [g.x, g.y]
}

print(json.dumps(payload))

Running the above code will give us the payload to send to the server. When we send this payload, the server will recognize the host as www.bing.com and return the flag.

ProSign 3

Challenge: This is my secure timestamp signing server. Only if you can produce a signature for "unlock" can you learn more.

Challenge files:

#!/usr/bin/env python3

import hashlib
from Crypto.Util.number import bytes_to_long, long_to_bytes
from ecdsa.ecdsa import Public_key, Private_key, Signature, generator_192
from utils import listener
from datetime import datetime
from random import randrange

FLAG = "crypto{?????????????????????????}"
g = generator_192
n = g.order()


class Challenge():
    def __init__(self):
        self.before_input = "Welcome to ProSign 3. You can sign_time or verify.\n"
        secret = randrange(1, n)
        self.pubkey = Public_key(g, g * secret)
        self.privkey = Private_key(self.pubkey, secret)

    def sha1(self, data):
        sha1_hash = hashlib.sha1()
        sha1_hash.update(data)
        return sha1_hash.digest()

    def sign_time(self):
        now = datetime.now()
        m, n = int(now.strftime("%m")), int(now.strftime("%S"))
        current = f"{m}:{n}"
        msg = f"Current time is {current}"
        hsh = self.sha1(msg.encode())
        sig = self.privkey.sign(bytes_to_long(hsh), randrange(1, n))
        return {"msg": msg, "r": hex(sig.r), "s": hex(sig.s)}

    def verify(self, msg, sig_r, sig_s):
        hsh = bytes_to_long(self.sha1(msg.encode()))
        sig_r = int(sig_r, 16)
        sig_s = int(sig_s, 16)
        sig = Signature(sig_r, sig_s)

        if self.pubkey.verifies(hsh, sig):
            return True
        else:
            return False

    #
    # This challenge function is called on your input, which must be JSON
    # encoded
    #
    def challenge(self, your_input):
        if 'option' not in your_input:
            return {"error": "You must send an option to this server"}

        elif your_input['option'] == 'sign_time':
            signature = self.sign_time()
            return signature

        elif your_input['option'] == 'verify':
            msg = your_input['msg']
            r = your_input['r']
            s = your_input['s']
            verified = self.verify(msg, r, s)
            if verified:
                if msg == "unlock":
                    self.exit = True
                    return {"flag": FLAG}
                return {"result": "Message verified"}
            else:
                return {"result": "Bad signature"}

        else:
            return {"error": "Decoding fail"}


import builtins; builtins.Challenge = Challenge # hack to enable challenge to be run locally, see https://cryptohack.org/faq/#listener
listener.start_server(port=13381)

Explain the source code: The main vulnerability is in the sign_time function. This function gets the current time (minutes and seconds) and uses it to create a message that is signed. But this function overwrites the variable n, which is the order of the generator point, with the current seconds value. This means that the signature is generated using a much smaller modulus, making it vulnerable to a brute-force attack.

The verify function verifies the signature for a given message. If the message is "unlock" and the signature is valid, it returns the flag.

Solution: In ECDSA, the s value of the signature is calculated as:

$$s \equiv k^{-1}(z + r \cdot d) \mod n$$

Where:

• $k$ is the random nonce used during signing.
• $z$ is the hash of the message.
• $r$ is part of the signature.
• $d$ is the private key.
• $n$ is the order of the generator point.

Attacking steps: First, we call sign_time to get a valid signature for the current time message. Then, we brute-force all the possible values of k (from 1 to 59). With each k, we can compute the private key d using the rearranged formula:

$$d = r^{-1}(s \cdot k - z) \mod n$$

After calculating, check d by asserting $d \cdot G = Q$, where $Q$ is the public key. Once we find the correct d, we can sign the message "unlock" and send it to the server to get the flag.

import hashlib
from Crypto.Util.number import bytes_to_long
from ecdsa.ecdsa import Public_key, Private_key, Signature, generator_192
import json
from pwn import remote

g = generator_192
N = g.order()

def sha1(data):
    sha1_hash = hashlib.sha1()
    sha1_hash.update(data)
    return sha1_hash.digest()

def solve():
    io = remote('socket.cryptohack.org', 13381)
    io.recvline()

    io.sendline(json.dumps({"option": "sign_time"}).encode())
    resp = json.loads(io.recvline().decode())
    
    msg = resp['msg']
    r = int(resp['r'], 16)
    s = int(resp['s'], 16)
    z = bytes_to_long(sha1(msg.encode()))

    d_found = None
    r_inv = pow(r, -1, N)

    for k_cand in range(1, 61):
        d_cand = (r_inv * (s * k_cand - z)) % N
        
        pubkey_cand = Public_key(g, g * d_cand)
        if pubkey_cand.verifies(z, Signature(r, s)):
            d_found = d_cand
            print(f"Private Key: {d_found}")
            break

    if not d_found:
        print("Not found")
        return

    privkey = Private_key(pubkey_cand, d_found)
    msg_unlock = "unlock"
    hsh_unlock = bytes_to_long(sha1(msg_unlock.encode()))
    
    sig_unlock = privkey.sign(hsh_unlock, 12345)
    
    payload = {
        "option": "verify",
        "msg": msg_unlock,
        "r": hex(sig_unlock.r),
        "s": hex(sig_unlock.s)
    }
    io.sendline(json.dumps(payload).encode())
    print(io.recvline().decode())

solve()