[CryptoHack] Public-key Cryptography

2025-12-22

Modular Exponentiation

All operations in RSA involve modular exponentiation. Together with the problem of prime factorization, they help us to build a "trapdoor function". This is a function that is easy to compute in one direction, but hard to reverse without special information. It allows us to encrypt a message, then only the person who has the key can decrypt it.

For example, calculating $101^{17} \mod 22663$

res = pow(101, 17, 22663)
print(res)

Public keys

RSA encryption is modular exponentiation of a message with an exponent $e$ and a modulus $n$ , which is a product of two large prime numbers $p$ and $q$ .

This is the public key: $(N, e)$ . The most common value for $e$ is $65537$ ( $0x10001$ ).

For example: Encrypt the number $12$ using the exponent $65537$ and the primes $p = 17$ and $q = 23$ .

p = 17
q = 23
n = p * q
e = 65537
message = 12

ciphertext = pow(message, e, n)
print(ciphertext)

Euler's totient

RSA relies on the difficulty of the prime factorization problem. If the prime factors of $N$ is deduced, then we can calculate Euler's totient function $\phi(N)$ and decrypt the message.

For example: Given $N = pq$ and two primes:

p = 857504083339712752489993810777
q = 1029224947942998075080348647219

Calculate $\phi(N)$ .

p = 857504083339712752489993810777
q = 1029224947942998075080348647219
n = p * q
phi_n = (p - 1) * (q - 1)
print(phi_n)

Private keys

The private keys $d$ is used to decrypt messages created with the corresponding public key $(N, e)$ . It's also used to sign a message.

In RSA, the private keys is the modular multiplicative inverse of $e$ modulo $\phi(N)$ .

For example: Given the two primes:

p = 857504083339712752489993810777
q = 1029224947942998075080348647219

and the exponent $e = 65537$ , calculate the private key $d = e^{-1} \mod \phi(N)$ .

p = 857504083339712752489993810777
q = 1029224947942998075080348647219
e = 65537
phi = (p - 1) * (q - 1)
d = pow(e, -1, phi)
print(d)

RSA Decryption

Use private key $d$ to decrypt a ciphertext $c$ using the formula: $m = c^d \mod N$ .

c = 77578995801157823671636298847186723593814843845525223303932
N = 882564595536224140639625987659416029426239230804614613279163
e = 65537

p = 857504083339712752489993810777
q = 1029224947942998075080348647219
phi = (p - 1) * (q - 1)
d = pow(e, -1, phi)

m = pow(c, d, N)
print(m)

RSA Signatures

How can you ensure that the person receiving your message know that you wrote it?

Maybe there is a situation that you send a message to your crush to invite her out for a date, but an jealous friend intercepts the message and changes it to something else. To prevent this, you can use digital signatures.

You write a message $m$ , you encrypt it with your friend's public key to create a ciphertext $c = m^{e_0} \mod N_0$ . To sign this message, you calculate the hash of the message $h = H(m)$ , then encrypt it with your private key to create the signature $S = h^{d_1} \mod N_1$ .

When your friend receives the message, she verify by the following steps:

Decrypt the message with her private key: $m = c^{d_0} \mod N_0$ .
Calculate the hash of the message: $h = H(m)$ .
Decrypt the signature with your public key to get $h' = s^{e_1} \mod N_1$ .
Compare $h$ and $h'. If they are the same, then the signature is valid.

For example, sign the flag: crypto{Immut4ble_m3ssag1ng} using your private key and SHA256 hash function.

N = 15216583654836731327639981224133918855895948374072384050848479908982286890731769486609085918857664046075375253168955058743185664390273058074450390236774324903305663479046566232967297765731625328029814055635316002591227570271271445226094919864475407884459980489638001092788574811554149774028950310695112688723853763743238753349782508121985338746755237819373178699343135091783992299561827389745132880022259873387524273298850340648779897909381979714026837172003953221052431217940632552930880000919436507245150726543040714721553361063311954285289857582079880295199632757829525723874753306371990452491305564061051059885803
d = 11175901210643014262548222473449533091378848269490518850474399681690547281665059317155831692300453197335735728459259392366823302405685389586883670043744683993709123180805154631088513521456979317628012721881537154107239389466063136007337120599915456659758559300673444689263854921332185562706707573660658164991098457874495054854491474065039621922972671588299315846306069845169959451250821044417886630346229021305410340100401530146135418806544340908355106582089082980533651095594192031411679866134256418292249592135441145384466261279428795408721990564658703903787956958168449841491667690491585550160457893350536334242689

message = b"crypto{Immut4ble_m3ssag1ng}"
hash = int.from_bytes(hashlib.sha256(message).digest(), "big")
signature = pow(hash, d, N)
print(signature)

Factoring

The security of RSA relies on the difficulty of factoring large numbers. It is easy to multiply two large prime numbers $p$ and $q$ to get $N$ . However, given $N$ , it is hard to find backward $p$ and $q$ .

So far, on above examples, we have used small prime numbers for simplicity. In reality, using primes that are at least 1024 bits long is recommended.

Multiplying two 1024-bit primes results in a 2048-bit modulus $N$ . As of 2024, factoring a 2048-bit number is considered computationally infeasible with current technology. Some say that in the future, we should use RSA-4096 or even RSA-8192 to ensure security.

However, more bits long, more computational power is required for encryption and decryption.

For example, factorise the 150-bit number 510143758735509025530880200653196460532653147 into its prime factors.

Use factordb, we can find two prime factors:

p = 19704762736204164635843
q = 25889363174021185185929

Now, we can verify that $N = pq$ :

p = 19704762736204164635843
q = 25889363174021185185929

N = p * q
if (N == 510143758735509025530880200653196460532653147):
    print("Correct N")
else:
    print("Incorrect N")

Monoprime

Now, let's give a question: Why we need to use two prime numbers $p$ and $q$ to generate $N$ ? Why not just use a single big prime number as $N$ ?

The answer is: RSA still works with any $N$ , but isn't secure. If $N$ is prime, then $\phi(N) = N - 1$ . Therefore, anyone can easily compute $\phi(N)$ , and then compute the private key $d$ from the public exponent $e$ .

Challenge: Find the flag.

n = 171731371218065444125482536302245915415603318380280392385291836472299752747934607246477508507827284075763910264995326010251268493630501989810855418416643352631102434317900028697993224868629935657273062472544675693365930943308086634291936846505861203914449338007760990051788980485462592823446469606824421932591                                                                  
e = 65537
ct = 161367550346730604451454756189028938964941280347662098798775466019463375610700074840105776873791605070092554650190486030367121011578171525759600774739890458414593857709994072516290998135846956596662071379067305011746842247628316996977338024343628757374524136260758515864509435302781735938531030576289086798942  

from Crypto.Util.number import long_to_bytes

phi = n - 1
d = pow(e, -1, phi)
pt = pow(ct, d, n)
flag = long_to_bytes(pt)
print(flag)

Manyprime

Challenge: Using one prime factor was definitely a bad idea so I'll try using over 30 instead.

Resources: Using ecm.factor in SageMath to factor n.

n = 580642391898843192929563856870897799650883152718761762932292482252152591279871421569162037190419036435041797739880389529593674485555792234900969402019055601781662044515999210032698275981631376651117318677368742867687180140048715627160641771118040372573575479330830092989800730105573700557717146251860588802509310534792310748898504394966263819959963273509119791037525504422606634640173277598774814099540555569257179715908642917355365791447508751401889724095964924513196281345665480688029639999472649549163147599540142367575413885729653166517595719991872223011969856259344396899748662101941230745601719730556631637
e = 65537
ct = 320721490534624434149993723527322977960556510750628354856260732098109692581338409999983376131354918370047625150454728718467998870322344980985635149656977787964380651868131740312053755501594999166365821315043312308622388016666802478485476059625888033017198083472976011719998333985531756978678758897472845358167730221506573817798467100023754709109274265835201757369829744113233607359526441007577850111228850004361838028842815813724076511058179239339760639518034583306154826603816927757236549096339501503316601078891287408682099750164720032975016814187899399273719181407940397071512493967454225665490162619270814464
factors = ecm.factor(n)
print(factors)

The prime factors are:

factors = [9282105380008121879, 9303850685953812323, 9389357739583927789, 10336650220878499841, 10638241655447339831, 11282698189561966721, 11328768673634243077, 11403460639036243901, 11473665579512371723, 11492065299277279799, 11530534813954192171, 11665347949879312361, 12132158321859677597, 12834461276877415051, 12955403765595949597, 12973972336777979701, 13099895578757581201, 13572286589428162097, 14100640260554622013, 14178869592193599187, 14278240802299816541, 14523070016044624039, 14963354250199553339, 15364597561881860737, 15669758663523555763, 15824122791679574573, 15998365463074268941, 16656402470578844539, 16898740504023346457, 17138336856793050757, 17174065872156629921, 17281246625998849649]

Use the factors to compute $\phi(N)$ , then decrypt the ciphertext to get the flag.

phi = 1
for p in factors:
    phi *= (p - 1)
    
d = pow(e, -1, phi)
pt = pow(ct, d, n)
print(bytes.fromhex(hex(pt)[2:]).decode())

Salty

Challenge: Smallest exponent should be fastest, right?

Source code:

#!/usr/bin/env python3

from Crypto.Util.number import getPrime, inverse, bytes_to_long, long_to_bytes

e = 1
d = -1

while d == -1:
    p = getPrime(512)
    q = getPrime(512)
    phi = (p - 1) * (q - 1)
    d = inverse(e, phi)

n = p * q

flag = b"XXXXXXXXXXXXXXXXXXXXXXX"
pt = bytes_to_long(flag)
ct = pow(pt, e, n)

print(f"n = {n}")
print(f"e = {e}")
print(f"ct = {ct}")

pt = pow(ct, d, n)
decrypted = long_to_bytes(pt)
assert decrypted == flag

Output:

n = 110581795715958566206600392161360212579669637391437097703685154237017351570464767725324182051199901920318211290404777259728923614917211291562555864753005179326101890427669819834642007924406862482343614488768256951616086287044725034412802176312273081322195866046098595306261781788276570920467840172004530873767                                                                  
e = 1
ct = 44981230718212183604274785925793145442655465025264554046028251311164494127485

In this challenge, the public exponent e is set to 1, which means the ciphertext is the same as the plaintext. Therefore, the flag can be directly obtained from the ciphertext.

from Crypto.Util.number import long_to_bytes
ct = 44981230718212183604274785925793145442655465025264554046028251311164494127485
flag = long_to_bytes(ct)
print(flag)

Modulus Inutilis

Challenge: My primes should be more than large enough now!

Source code:

#!/usr/bin/env python3

from Crypto.Util.number import getPrime, inverse, bytes_to_long, long_to_bytes

e = 3
d = -1

while d == -1:
    p = getPrime(1024)
    q = getPrime(1024)
    phi = (p - 1) * (q - 1)
    d = inverse(e, phi)

n = p * q

flag = b"XXXXXXXXXXXXXXXXXXXXXXX"
pt = bytes_to_long(flag)
ct = pow(pt, e, n)

print(f"n = {n}")
print(f"e = {e}")
print(f"ct = {ct}")

pt = pow(ct, d, n)
decrypted = long_to_bytes(pt)
assert decrypted == flag

Output:

n = 17258212916191948536348548470938004244269544560039009244721959293554822498047075403658429865201816363311805874117705688359853941515579440852166618074161313773416434156467811969628473425365608002907061241714688204565170146117869742910273064909154666642642308154422770994836108669814632309362483307560217924183202838588431342622551598499747369771295105890359290073146330677383341121242366368309126850094371525078749496850520075015636716490087482193603562501577348571256210991732071282478547626856068209192987351212490642903450263288650415552403935705444809043563866466823492258216747445926536608548665086042098252335883
e = 3
ct = 243251053617903760309941844835411292373350655973075480264001352919865180151222189820473358411037759381328642957324889519192337152355302808400638052620580409813222660643570085177957

In this challenge, the public exponent $e$ is set to 3, which is very small. The formular to encrypt a message is $c = m^e \mod N$ , which is $c = m^3 \mod N$ in this case. Therefore, if the message $m$ is small enough such that $m^3 < N$ , then the ciphertext $c$ is simply equal to $m^3$ . We can easily recover the plaintext by calculating the integer cube root of the ciphertext.

from Crypto.Util.number import long_to_bytes
import gmpy2

n = 17258212916191948536348548470938004244269544560039009244721959293554822498047075403658429865201816363311805874117705688359853941515579440852166618074161313773416434156467811969628473425365608002907061241714688204565170146117869742910273064909154666642642308154422770994836108669814632309362483307560217924183202838588431342622551598499747369771295105890359290073146330677383341121242366368309126850094371525078749496850520075015636716490087482193603562501577348571256210991732071282478547626856068209192987351212490642903450263288650415552403935705444809043563866466823492258216747445926536608548665086042098252335883
e = 3
ct = 243251053617903760309941844835411292373350655973075480264001352919865180151222189820473358411037759381328642957324889519192337152355302808400638052620580409813222660643570085177957

pt, exact = gmpy2.iroot(ct, 3)

if exact:
    print(f"Flag: {long_to_bytes(int(pt)).decode()}")

Working with Fields

The set of integers modulo $N$ forms a Ring. This means you can perform addition, multiplication, the result will always be in the set.

However, not all elements in the ring have a multiplicative inverse. For example, in the ring of integers modulo $8$ , the number $4$ does not have an inverse because there is no integer $x$ such that $4x \equiv 1 \mod 8$ .

To ensure that every non-zero element has a multiplicative inverse, we work in a Field. In RSA, we often work in the field of integers modulo a prime number $p$ . In this field, every non-zero element has an inverse.

For example: Givem the prime $p = 991$ , and the element $g = 209$ , find the inverse element $d = g^{-1}$ such that $g \cdot d \equiv 1 \mod p$ .

d = pow(209, -1, 991)
print(d)

Generators of Groups

In a finite field, every elements can be used to make a subgroup $H$ by repeatedly multiplying the element by itself. In other words, for an element $g$ in a field $F$ , we can create a subgroup $H = \{ g^0, g^1, g^2, ... \}$ .

If this subgroup $H$ contains all non-zero elements of the field $F$ , then $g$ is called a generator of the field.

For example: Given $p = 7$ , if we choose $g = 3$ , then the subgroup generated by $g$ is:

H = \{ 3^0 \mod 7, 3^1 \mod 7, 3^2 \mod 7, 3^3 \mod 7, 3^4 \mod 7, 3^5 \mod 7 \} = \{ 1, 3, 2, 6, 4, 5 \}

Since $H$ contains all non-zero elements of the field of integers modulo $7$ , $g = 3$ is a generator of the field.

Challenge: For the finite field with $p = 28151$ , find the smallest generator $g$ .

Solution: We have two ways to check if an element $g$ is a generator of the field:

Brute-force method: Generate the subgroup $H$ by repeatedly multiplying $g$ by itself until we reach $1$ again. If the size of $H$ is equal to $p - 1$ , then $g$ is a generator.

def is_generator(g, p):
    current = g
    order = 1
    while current != 1:
        current = (current * g) % p
        order += 1
        if order > p - 1:  
            return False
    return order == p - 1

if __name__ == "__main__":
    p = 28151  
    for g in range(2, p):
        if is_generator(g, p):
            print(g)
            break

Math: A number $g$ is a generator of the field if for every prime factor $q$ of $p - 1$ , the following condition holds:

g^{(p - 1) / q} \mod p \neq 1

p = 28151
factors = [2, 25, 563]

for g in range(2, p-1):
    if (pow(g, (p - 1) // factors[0], p) != 1 and
        pow(g, (p - 1) // factors[1], p) != 1 and
        pow(g, (p - 1) // factors[2], p) != 1):
        print(g)
        break

Computing Public Values

Diffe-Hellman key exchange protocol is used to securely share a secret key between two parties over an insecure channel. The protocol relies on the difficulty of the discrete logarithm problem in finite fields:

A \equiv g^a \mod p

It's easy to calculate $A$ given $g$ , $a$ , and $p$ . However, given $A$ , $g$ , and $p$ , it's hard to find $a$ .

Notes for parameters:

$p$ is a large prime number. It may be a safe prime, for example, $p = 2q + 1$ where $q$ is also prime. This choice can prevent attacks like Pohlig-Hellman.
$g$ is a generator of the multiplicative group of integers modulo $p$ . It should be chosen such that it generates a large subgroup to ensure security.
$a$ is a private key, chosen randomly from the range $[1, p-2]$ .
$A$ is the public value, calculated as $A \equiv g^a \mod p$ .

For example: Given the parameters:

g: 2
p: 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919

Calculate the value of $g^a \mod p$ for the private key:

a: 972107443837033796245864316200458246846904598488981605856765890478853088246897345487328491037710219222038930943365848626194109830309179393018216763327572120124760140018038673999837643377590434413866611132403979547150659053897355593394492586978400044375465657296027592948349589216415363722668361328689588996541370097559090335137676411595949335857341797148926151694299575970292809805314431447043469447485957669949989090202320234337890323293401862304986599884732815

Solution:

g = 2
p = 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919
a = 972107443837033796245864316200458246846904598488981605856765890478853088246897345487328491037710219222038930943365848626194109830309179393018216763327572120124760140018038673999837643377590434413866611132403979547150659053897355593394492586978400044375465657296027592948349589216415363722668361328689588996541370097559090335137676411595949335857341797148926151694299575970292809805314431447043469447485957669949989090202320234337890323293401862304986599884732815

g_a = pow(g, a, p)
print(g_a)

Computing Shared Secrets

After exchanging public values, both parties can compute the shared secret key without sending it via Internet.

Imagine, you are Bob and you are communicating with Alice. There are the parameters:

$p$ and $g$ are public parameters of NIST.
$A$ is Alice's public value, calculated from her secret value $a$ and sent to you.
$b$ is your private key, chosen randomly.
$B$ is your public value, calculated from your private key $b$ and sent to Alice.

Now, you can compute the shared secret $s$ using Alice's public value $A$ and your private key $b$ :

S = A^b \mod p

Why does this work? Because Alice can also compute the same shared secret using your public value $B$ and her private key $a$ :

Alice computes:

S = B^a \mod p = (g^b)^a \mod p = g^{ab} \mod p

Bob computes:

S = A^b \mod p = (g^a)^b \mod p = g^{ab} \mod p

Both values of Alice and Bob are always the same.

For example, using the parameters and calculate the shared secret $s$ .

g = 2
p = 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919
A = 70249943217595468278554541264975482909289174351516133994495821400710625291840101960595720462672604202133493023241393916394629829526272643847352371534839862030410331485087487331809285533195024369287293217083414424096866925845838641840923193480821332056735592483730921055532222505605661664236182285229504265881752580410194731633895345823963910901731715743835775619780738974844840425579683385344491015955892106904647602049559477279345982530488299847663103078045601
b = 12019233252903990344598522535774963020395770409445296724034378433497976840167805970589960962221948290951873387728102115996831454482299243226839490999713763440412177965861508773420532266484619126710566414914227560103715336696193210379850575047730388378348266180934946139100479831339835896583443691529372703954589071507717917136906770122077739814262298488662138085608736103418601750861698417340264213867753834679359191427098195887112064503104510489610448294420720
B = 518386956790041579928056815914221837599234551655144585133414727838977145777213383018096662516814302583841858901021822273505120728451788412967971809038854090670743265187138208169355155411883063541881209288967735684152473260687799664130956969450297407027926009182761627800181901721840557870828019840218548188487260441829333603432714023447029942863076979487889569452186257333512355724725941390498966546682790608125613166744820307691068563387354936732643569654017172

s = pow(A, b, p)
print(s)

Deriving Symmetric Keys

Challenge: Alice sends Bob the following IV and ciphertext:

{
    'iv': '737561146ff8194f45290f5766ed6aba', 
    'encrypted_flag': '39c99bf2f0c14678d6a5416faef954b5893c316fc3c48622ba1fd6a9fe85f3dc72a29c394cf4bc8aff6a7b21cae8e12c'
}

The values $p$ , $g$ , $A$ , $B$ and $b$ are given.

The encrypt source code is as follows:

from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
import hashlib
import os
from secret import shared_secret

FLAG = b'crypto{????????????????????????????}'


def encrypt_flag(shared_secret: int):
    # Derive AES key from shared secret
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    # Encrypt flag
    iv = os.urandom(16)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    ciphertext = cipher.encrypt(pad(FLAG, 16))
    # Prepare data to send
    data = {}
    data['iv'] = iv.hex()
    data['encrypted_flag'] = ciphertext.hex()
    return data


print(encrypt_flag(shared_secret))

Explain the encryption process:

First, Alice get the value of shared_secret and convert it to string, then encode it to bytes using ASCII encoding.
Next, she computes the SHA-1 hash of the byte representation of the shared secret. The first 16 bytes of the hash digest are used as the AES key for encryption.
Alice uses AES encryption in CBC mode with a randomly generated initialization vector (IV) to encrypt the flag. The flag is padded to ensure its length is a multiple of the AES block size (16 bytes).

To decrypt the ciphertext and retrieve the flag, follow these steps:

Compute the shared secret using the given values of $p$ , $g$ , $A$ , $B$ , and $b$ .
Derive the AES key from the shared secret using the same method as Alice.
Use the derived AES key and the provided IV to decrypt the ciphertext.

There is a template code for decryption as follows:

import hashlib
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad


g = 2
p = 2410312426921032588552076022197566074856950548502459942654116941958108831682612228890093858261341614673227141477904012196503648957050582631942730706805009223062734745341073406696246014589361659774041027169249453200378729434170325843778659198143763193776859869524088940195577346119843545301547043747207749969763750084308926339295559968882457872412993810129130294592999947926365264059284647209730384947211681434464714438488520940127459844288859336526896320919633919
A = 112218739139542908880564359534373424013016249772931962692237907571990334483528877513809272625610512061159061737608547288558662879685086684299624481742865016924065000555267977830144740364467977206555914781236397216033805882207640219686011643468275165718132888489024688846101943642459655423609111976363316080620471928236879737944217503462265615774774318986375878440978819238346077908864116156831874695817477772477121232820827728424890845769152726027520772901423784
b = 197395083814907028991785772714920885908249341925650951555219049411298436217190605190824934787336279228785809783531814507661385111220639329358048196339626065676869119737979175531770768861808581110311903548567424039264485661330995221907803300824165469977099494284722831845653985392791480264712091293580274947132480402319812110462641143884577706335859190668240694680261160210609506891842793868297672619625924001403035676872189455767944077542198064499486164431451944
B = 1241972460522075344783337556660700537760331108332735677863862813666578639518899293226399921252049655031563612905395145236854443334774555982204857895716383215705498970395379526698761468932147200650513626028263449605755661189525521343142979265044068409405667549241125597387173006460145379759986272191990675988873894208956851773331039747840312455221354589910726982819203421992729738296452820365553759182547255998984882158393688119629609067647494762616719047466973581


s = pow(A, b, p)

def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')


shared_secret = s
iv = '737561146ff8194f45290f5766ed6aba'
ciphertext = '39c99bf2f0c14678d6a5416faef954b5893c316fc3c48622ba1fd6a9fe85f3dc72a29c394cf4bc8aff6a7b21cae8e12c'

print(decrypt_flag(shared_secret, iv, ciphertext))

Parameter Injection

Challenge: You're in a position to not only intercept Alice and Bob's DH key exchange, but also rewrite their messages. Think about how you can play with the DH equation that they calculate, and therefore sidestep the need to crack any discrete logarithm problem.

Use the script from "Deriving Symmetric Keys" to decrypt the flag once you've recovered the shared secret.

Connect at socket.cryptohack.org 13371

Solution:

We have some ways to manipulate the parameters exchanged between Alice and Bob to force the shared secret to a known value.

For example, we can send $A$ = $p$ to Bob and $B$ = $p$ to Alice. Both parties will compute the shared secret as follows:

S = A^b \mod p = p^b \mod p = 0

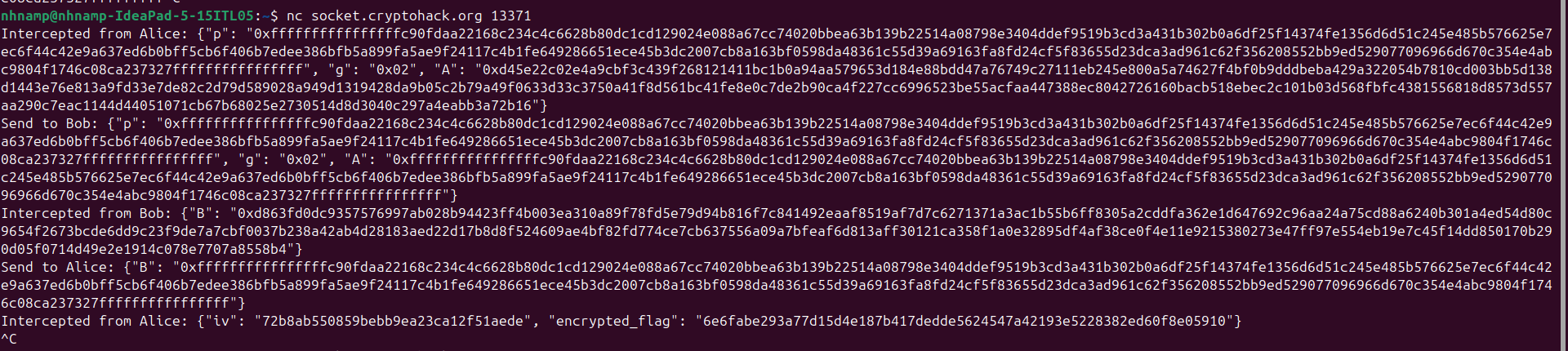
alt text

After intercepting and modifying the messages, we can use the known shared secret 0, iv and ciphertext to decrypt the flag using the decryption code provided in the "Deriving Symmetric Keys" section.

import hashlib
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad


def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')


shared_secret = 0
iv = '72b8ab550859bebb9ea23ca12f51aede'
ciphertext = '6e6fabe293a77d15d4e187b417dedde5624547a42193e5228382ed60f8e05910'

print(decrypt_flag(shared_secret, iv, ciphertext))

Export-grade

Challenge: Alice and Bob are using legacy codebases and need to negotiate parameters they both support. You've man-in-the-middled this negotiation step, and can passively observe thereafter. How are you going to ruin their day this time?

This is the entire process:

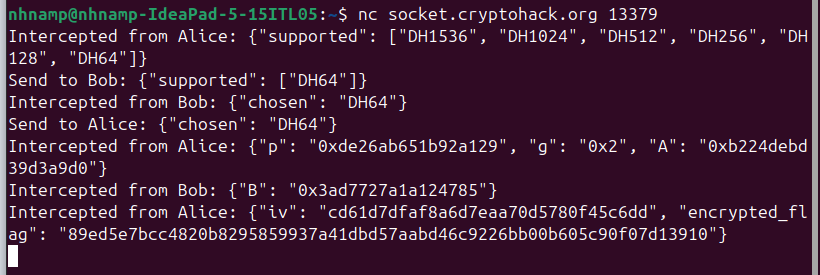
alt text

When connecting to the server, we can see the intercepted message from Alice, which contains supported protocols. We can modify this message to only include the weakest protocol DH64.

Then, we obtain the parameters $p$ , $g$ , $A$ , $B$ from the server. With a small prime $p$ (64 bits), we can easily compute the private keys $a$ and $b$ .

Finally, we can compute the shared secret $s$ and use it to decrypt the ciphertext to get the flag.

First, using SageMath to compute the private key $a$ :

p = 0xde26ab651b92a129
g = 2
A = 0xb224debd39d3a9d0
a = discrete_log(mod(A, p), mod(g, p))
print(a)

Then, using python script to compute the shared secret and decrypt the flag:

import hashlib
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad

a = 3269154780776244393
B = 0x3ad7727a1a124785
p = 0xde26ab651b92a129

s = pow(B, a, p)

def is_pkcs7_padded(message):
    padding = message[-message[-1]:]
    return all(padding[i] == len(padding) for i in range(0, len(padding)))


def decrypt_flag(shared_secret: int, iv: str, ciphertext: str):
    sha1 = hashlib.sha1()
    sha1.update(str(shared_secret).encode('ascii'))
    key = sha1.digest()[:16]
    ciphertext = bytes.fromhex(ciphertext)
    iv = bytes.fromhex(iv)
    cipher = AES.new(key, AES.MODE_CBC, iv)
    plaintext = cipher.decrypt(ciphertext)

    if is_pkcs7_padded(plaintext):
        return unpad(plaintext, 16).decode('ascii')
    else:
        return plaintext.decode('ascii')


shared_secret = s
iv = 'cd61d7dfaf8a6d7eaa70d5780f45c6dd'
ciphertext = '89ed5e7bcc4820b8295859937a41dbd57aabd46c9226bb00b605c90f07d13910'

print(decrypt_flag(shared_secret, iv, ciphertext))

This is the end of the Public-key Cryptography module on CryptoHack. Thanks for a great course!