[CryptoHack] Symmetric Cryptography
Overview
Symmetric-key ciphers are algorithms that use the same key both to encrypt and decrypt data. The goal is to use short secret keys to securely and efficiently send long messages.
In this course, we are mainly guided through the inner workings of AES (Advanced Encryption Standard).
We can split symmetric-key ciphers into 2 types: block ciphers and stream ciphers.
- Block ciphers break up a plaintext into fixed-length blocks and send each block through an encryption function together with a secret key.
- Stream ciphers encrypt one byte of plaintext at a time, for example, using the XOR operation with a random keystream.
- AES is a block cipher, but can be turned into a stream cipher using modes of operation.
How AES works
Keyed Permutations
AES performs a “keyed permutation”; this means that it maps every possible input block to a unique output block, with a key determining which permutation is used.
A block in AES refers to a fixed number of bits or bytes. For example, AES works on a block of 128 bits and a 128-bit key; it’s called AES-128.
One-to-one correspondence: One plaintext block will be encrypted to only one ciphertext block. This is called “bijection”.
Resisting Brute-force
Brute-force: try every possible key.
But it’s very difficult to make a brute-force attack on a 128-bit key space. There is an attack on AES that is better than brute-force, by lowering the security level of AES-128 down to 126.1 bits.
In the era of quantum computers, the security of AES is reduced by approximately half. That is why people recommend using AES-256; despite it being less secure, it would still provide a very adequate 128 bits of security in a quantum future.
Structure of AES
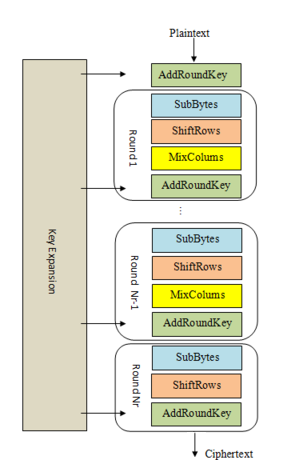
The ciphertext is divided into blocks, each block is 128-bit length (with AES-128), and displayed as a 4x4 matrix.
1. Key Expansion:
From a 128-bit key, the algorithm creates 11 “round keys”; each key is also 128 bits in length. There is one key that is used for AddRoundKey.
2. Initial AddRoundKey:
The first bytes of the first round key are taken into a XOR operation with the bytes of the plaintext in matrix format.
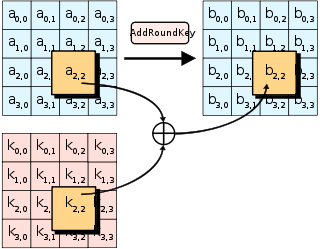
3. Rounds:
a. SubBytes:
Each byte of the matrix is substituted with another byte according to an S-box (a pre-defined dictionary for substitution).
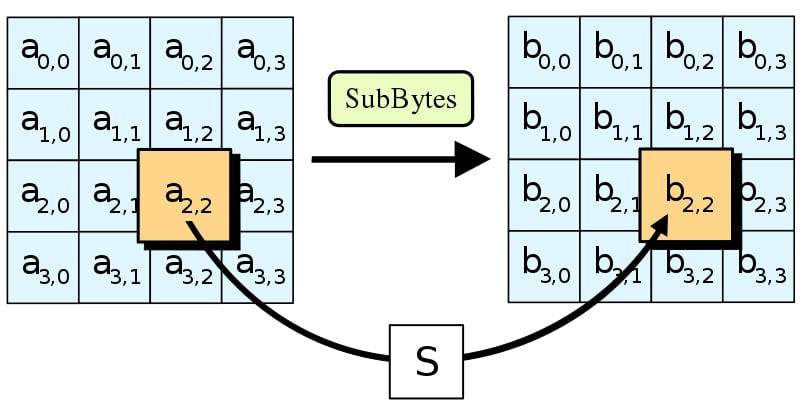
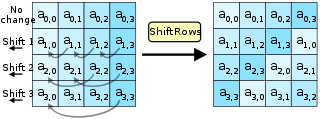
b. ShiftRows:
The last 3 rows of the matrix are permutated. In detail, the rows are shifted left: the second row is 1-byte shifted, the third row is 2-byte shifted, and the fourth row is 3-byte shifted.
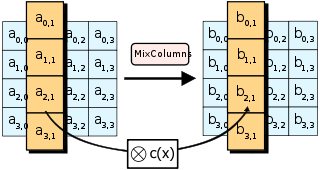
c. MixColumns:
A matrix multiplication is performed on each column of the matrix, mixing 4 bytes on each column together. This step is to diffuse vertically.
This step is ignored in the last round.
d. AddRoundKey:
Bytes of the current round key are taken on an XOR operation with the bytes of the matrix (The same as 2).
After finishing 10 rounds, the final matrix is the ciphertext.
Round Keys
Like the previous description. There is some code:
def bytes2matrix(text):
""" Converts a 16-byte array into a 4x4 matrix. """
return [list(text[i:i+4]) for i in range(0, len(text), 4)]
def matrix2bytes(matrix):
""" Converts a 4x4 matrix into a 16-byte array. """
return bytes(sum(matrix, []))
state = [
[206, 243, 61, 34],
[171, 11, 93, 31],
[16, 200, 91, 108],
[150, 3, 194, 51],
]
round_key = [
[173, 129, 68, 82],
[223, 100, 38, 109],
[32, 189, 53, 8],
[253, 48, 187, 78],
]
def add_round_key(s, k):
new_state = []
for i in range(4):
new_state.append([s[i][j] ^ k[i][j] for j in range(4)])
return new_state
print(matrix2bytes(add_round_key(state, round_key))) # crypto{r0undk3y}
Confusion through Substitution
In 1945, the mathematician Claude Shannon published a theory that the higher the confusion in ciphers, the harder they become to break.
The confusion means the relationship between the ciphertext and the key should be complicated. In other words, given a ciphertext will not lead to key guessing. For example, the Caesar cipher has an obvious relation: . So it’s very easy to guess the key. In higher levels, the ciphers that are based on linear transformation are also easy to break.
The S-box in AES follows this theory. The main purpose of the S-box is to transform the input in a way that is resistant to being approximated by linear functions. S-boxes aim for non-linear relations.
The fast lookup in an S-box is a shortcut for performing a very nonlinear function on the input bytes. This function involves taking the modular inverse in the Galois field 2**8 and then applying an affine transformation which has been tweaked for maximum confusion. The simplest way to express the function is through the following high-degree polynomial:
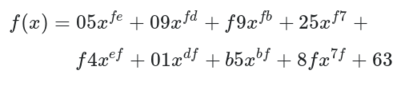
To make the S-box, the function has been calculated on all input values from 0x00 to 0xff, and the outputs have been put in the lookup table.
For example:
s_box = (
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
inv_s_box = (
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)
state = [
[251, 64, 182, 81],
[146, 168, 33, 80],
[199, 159, 195, 24],
[64, 80, 182, 255],
]
def sub_bytes(s, sbox=s_box):
return [[sbox[b] for b in row] for row in s]
print(sub_bytes(state, sbox=inv_s_box))
print(bytes(sum(sub_bytes(state, sbox=inv_s_box), [])))
s_box : Each value in state is passed through the sub_bytes function as the index of s_box. For example, the first element of s_box is 251, the returned value from the sub_bytes function will be the 251st number of the s_box table.
Otherwise, when the lookup table inv_s_box is used, it returns the initial value of state.
Diffusion through Permutation
Another property described by Shannon is diffusion. This relates to how every part of a cipher’s input should spread to every part of the output.
Imagine that the AES algorithm only has the S-box step. In this situation, if we change only 1 byte at 1 position (for example, [1, 1]), after rounds, only this byte is changed. Therefore, the first byte of the ciphertext only depends on the first byte of the plaintext. This allows cryptanalysts to break 16 simple 8-bit ciphers in parallel.
To prevent this weakness, the AES algorithm uses 2 permutation steps after the S-box step: ShiftRows and MixColumns. These two steps work together to ensure every byte affects every other byte in the state matrix within just two rounds.
ShiftRows:
MixColumns:
Code for simulation:
def shift_rows(s):
s[0][1], s[1][1], s[2][1], s[3][1] = s[1][1], s[2][1], s[3][1], s[0][1]
s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
s[0][3], s[1][3], s[2][3], s[3][3] = s[3][3], s[0][3], s[1][3], s[2][3]
def inv_shift_rows(s):
s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)
def mix_single_column(a):
# see Sec 4.1.2 in The Design of Rijndael
t = a[0] ^ a[1] ^ a[2] ^ a[3]
u = a[0]
a[0] ^= t ^ xtime(a[0] ^ a[1])
a[1] ^= t ^ xtime(a[1] ^ a[2])
a[2] ^= t ^ xtime(a[2] ^ a[3])
a[3] ^= t ^ xtime(a[3] ^ u)
def mix_columns(s):
for i in range(4):
mix_single_column(s[i])
def inv_mix_columns(s):
# see Sec 4.1.3 in The Design of Rijndael
for i in range(4):
u = xtime(xtime(s[i][0] ^ s[i][2]))
v = xtime(xtime(s[i][1] ^ s[i][3]))
s[i][0] ^= u
s[i][1] ^= v
s[i][2] ^= u
s[i][3] ^= v
mix_columns(s)
state = [
[108, 106, 71, 86],
[96, 62, 38, 72],
[42, 184, 92, 209],
[94, 79, 8, 54],
]
inv_mix_columns(state)
inv_shift_rows(state)
for row in state:
print(" ".join(chr(x) for x in row), end="") # c r y pt o { d1 f f Us 3 R }
Complete code for AES decryption
N_ROUNDS = 10
key = b'\xc3,\\\xa6\xb5\x80^\x0c\xdb\x8d\xa5z*\xb6\xfe\\'
ciphertext = b'\xd1O\x14j\xa4+O\xb6\xa1\xc4\x08B)\x8f\x12\xdd'
s_box = (
0x63, 0x7C, 0x77, 0x7B, 0xF2, 0x6B, 0x6F, 0xC5, 0x30, 0x01, 0x67, 0x2B, 0xFE, 0xD7, 0xAB, 0x76,
0xCA, 0x82, 0xC9, 0x7D, 0xFA, 0x59, 0x47, 0xF0, 0xAD, 0xD4, 0xA2, 0xAF, 0x9C, 0xA4, 0x72, 0xC0,
0xB7, 0xFD, 0x93, 0x26, 0x36, 0x3F, 0xF7, 0xCC, 0x34, 0xA5, 0xE5, 0xF1, 0x71, 0xD8, 0x31, 0x15,
0x04, 0xC7, 0x23, 0xC3, 0x18, 0x96, 0x05, 0x9A, 0x07, 0x12, 0x80, 0xE2, 0xEB, 0x27, 0xB2, 0x75,
0x09, 0x83, 0x2C, 0x1A, 0x1B, 0x6E, 0x5A, 0xA0, 0x52, 0x3B, 0xD6, 0xB3, 0x29, 0xE3, 0x2F, 0x84,
0x53, 0xD1, 0x00, 0xED, 0x20, 0xFC, 0xB1, 0x5B, 0x6A, 0xCB, 0xBE, 0x39, 0x4A, 0x4C, 0x58, 0xCF,
0xD0, 0xEF, 0xAA, 0xFB, 0x43, 0x4D, 0x33, 0x85, 0x45, 0xF9, 0x02, 0x7F, 0x50, 0x3C, 0x9F, 0xA8,
0x51, 0xA3, 0x40, 0x8F, 0x92, 0x9D, 0x38, 0xF5, 0xBC, 0xB6, 0xDA, 0x21, 0x10, 0xFF, 0xF3, 0xD2,
0xCD, 0x0C, 0x13, 0xEC, 0x5F, 0x97, 0x44, 0x17, 0xC4, 0xA7, 0x7E, 0x3D, 0x64, 0x5D, 0x19, 0x73,
0x60, 0x81, 0x4F, 0xDC, 0x22, 0x2A, 0x90, 0x88, 0x46, 0xEE, 0xB8, 0x14, 0xDE, 0x5E, 0x0B, 0xDB,
0xE0, 0x32, 0x3A, 0x0A, 0x49, 0x06, 0x24, 0x5C, 0xC2, 0xD3, 0xAC, 0x62, 0x91, 0x95, 0xE4, 0x79,
0xE7, 0xC8, 0x37, 0x6D, 0x8D, 0xD5, 0x4E, 0xA9, 0x6C, 0x56, 0xF4, 0xEA, 0x65, 0x7A, 0xAE, 0x08,
0xBA, 0x78, 0x25, 0x2E, 0x1C, 0xA6, 0xB4, 0xC6, 0xE8, 0xDD, 0x74, 0x1F, 0x4B, 0xBD, 0x8B, 0x8A,
0x70, 0x3E, 0xB5, 0x66, 0x48, 0x03, 0xF6, 0x0E, 0x61, 0x35, 0x57, 0xB9, 0x86, 0xC1, 0x1D, 0x9E,
0xE1, 0xF8, 0x98, 0x11, 0x69, 0xD9, 0x8E, 0x94, 0x9B, 0x1E, 0x87, 0xE9, 0xCE, 0x55, 0x28, 0xDF,
0x8C, 0xA1, 0x89, 0x0D, 0xBF, 0xE6, 0x42, 0x68, 0x41, 0x99, 0x2D, 0x0F, 0xB0, 0x54, 0xBB, 0x16,
)
inv_s_box = (
0x52, 0x09, 0x6A, 0xD5, 0x30, 0x36, 0xA5, 0x38, 0xBF, 0x40, 0xA3, 0x9E, 0x81, 0xF3, 0xD7, 0xFB,
0x7C, 0xE3, 0x39, 0x82, 0x9B, 0x2F, 0xFF, 0x87, 0x34, 0x8E, 0x43, 0x44, 0xC4, 0xDE, 0xE9, 0xCB,
0x54, 0x7B, 0x94, 0x32, 0xA6, 0xC2, 0x23, 0x3D, 0xEE, 0x4C, 0x95, 0x0B, 0x42, 0xFA, 0xC3, 0x4E,
0x08, 0x2E, 0xA1, 0x66, 0x28, 0xD9, 0x24, 0xB2, 0x76, 0x5B, 0xA2, 0x49, 0x6D, 0x8B, 0xD1, 0x25,
0x72, 0xF8, 0xF6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xD4, 0xA4, 0x5C, 0xCC, 0x5D, 0x65, 0xB6, 0x92,
0x6C, 0x70, 0x48, 0x50, 0xFD, 0xED, 0xB9, 0xDA, 0x5E, 0x15, 0x46, 0x57, 0xA7, 0x8D, 0x9D, 0x84,
0x90, 0xD8, 0xAB, 0x00, 0x8C, 0xBC, 0xD3, 0x0A, 0xF7, 0xE4, 0x58, 0x05, 0xB8, 0xB3, 0x45, 0x06,
0xD0, 0x2C, 0x1E, 0x8F, 0xCA, 0x3F, 0x0F, 0x02, 0xC1, 0xAF, 0xBD, 0x03, 0x01, 0x13, 0x8A, 0x6B,
0x3A, 0x91, 0x11, 0x41, 0x4F, 0x67, 0xDC, 0xEA, 0x97, 0xF2, 0xCF, 0xCE, 0xF0, 0xB4, 0xE6, 0x73,
0x96, 0xAC, 0x74, 0x22, 0xE7, 0xAD, 0x35, 0x85, 0xE2, 0xF9, 0x37, 0xE8, 0x1C, 0x75, 0xDF, 0x6E,
0x47, 0xF1, 0x1A, 0x71, 0x1D, 0x29, 0xC5, 0x89, 0x6F, 0xB7, 0x62, 0x0E, 0xAA, 0x18, 0xBE, 0x1B,
0xFC, 0x56, 0x3E, 0x4B, 0xC6, 0xD2, 0x79, 0x20, 0x9A, 0xDB, 0xC0, 0xFE, 0x78, 0xCD, 0x5A, 0xF4,
0x1F, 0xDD, 0xA8, 0x33, 0x88, 0x07, 0xC7, 0x31, 0xB1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xEC, 0x5F,
0x60, 0x51, 0x7F, 0xA9, 0x19, 0xB5, 0x4A, 0x0D, 0x2D, 0xE5, 0x7A, 0x9F, 0x93, 0xC9, 0x9C, 0xEF,
0xA0, 0xE0, 0x3B, 0x4D, 0xAE, 0x2A, 0xF5, 0xB0, 0xC8, 0xEB, 0xBB, 0x3C, 0x83, 0x53, 0x99, 0x61,
0x17, 0x2B, 0x04, 0x7E, 0xBA, 0x77, 0xD6, 0x26, 0xE1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0C, 0x7D,
)
def bytes2matrix(text):
""" Converts a 16-byte array into a 4x4 matrix. """
return [list(text[i:i+4]) for i in range(0, len(text), 4)]
def matrix2bytes(matrix):
return bytes(sum(matrix, []))
def inv_shift_rows(s):
s[0][1], s[1][1], s[2][1], s[3][1] = s[3][1], s[0][1], s[1][1], s[2][1]
s[0][2], s[1][2], s[2][2], s[3][2] = s[2][2], s[3][2], s[0][2], s[1][2]
s[0][3], s[1][3], s[2][3], s[3][3] = s[1][3], s[2][3], s[3][3], s[0][3]
def inv_sub_bytes(s):
""" Applies the inverse S-box to each byte of the state. """
for i in range(4):
for j in range(4):
s[i][j] = inv_s_box[s[i][j]]
def add_round_key(s, k):
""" Adds the round key to the state by an XOR function. """
for i in range(4):
for j in range(4):
s[i][j] ^= k[i][j]
xtime = lambda a: (((a << 1) ^ 0x1B) & 0xFF) if (a & 0x80) else (a << 1)
def mix_single_column(a):
# see Sec 4.1.2 in The Design of Rijndael
t = a[0] ^ a[1] ^ a[2] ^ a[3]
u = a[0]
a[0] ^= t ^ xtime(a[0] ^ a[1])
a[1] ^= t ^ xtime(a[1] ^ a[2])
a[2] ^= t ^ xtime(a[2] ^ a[3])
a[3] ^= t ^ xtime(a[3] ^ u)
def mix_columns(s):
for i in range(4):
mix_single_column(s[i])
def inv_mix_columns(s):
# see Sec 4.1.3 in The Design of Rijndael
for i in range(4):
u = xtime(xtime(s[i][0] ^ s[i][2]))
v = xtime(xtime(s[i][1] ^ s[i][3]))
s[i][0] ^= u
s[i][1] ^= v
s[i][2] ^= u
s[i][3] ^= v
mix_columns(s)
def expand_key(master_key):
"""
Expands and returns a list of key matrices for the given master_key.
"""
# Round constants https://en.wikipedia.org/wiki/AES_key_schedule#Round_constants
r_con = (
0x00, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40,
0x80, 0x1B, 0x36, 0x6C, 0xD8, 0xAB, 0x4D, 0x9A,
0x2F, 0x5E, 0xBC, 0x63, 0xC6, 0x97, 0x35, 0x6A,
0xD4, 0xB3, 0x7D, 0xFA, 0xEF, 0xC5, 0x91, 0x39,
)
# Initialize round keys with raw key material.
key_columns = bytes2matrix(master_key)
iteration_size = len(master_key) // 4
# Each iteration has exactly as many columns as the key material.
i = 1
while len(key_columns) < (N_ROUNDS + 1) * 4:
# Copy previous word.
word = list(key_columns[-1])
# Perform schedule_core once every "row".
if len(key_columns) % iteration_size == 0:
# Circular shift.
word.append(word.pop(0))
# Map to S-BOX.
word = [s_box[b] for b in word]
# XOR with first byte of R-CON, since the others bytes of R-CON are 0.
word[0] ^= r_con[i]
i += 1
elif len(master_key) == 32 and len(key_columns) % iteration_size == 4:
# Run word through S-box in the fourth iteration when using a
# 256-bit key.
word = [s_box[b] for b in word]
# XOR with equivalent word from previous iteration.
word = bytes(i^j for i, j in zip(word, key_columns[-iteration_size]))
key_columns.append(word)
# Group key words in 4x4 byte matrices.
return [key_columns[4*i : 4*(i+1)] for i in range(len(key_columns) // 4)]
def decrypt(key, ciphertext):
round_keys = expand_key(key) # Remember to start from the last round key and work backwards through them when decrypting
# Convert ciphertext to state matrix
state = bytes2matrix(ciphertext)
# Initial add round key step
add_round_key(state, round_keys[-1])
for i in range(N_ROUNDS - 1, 0, -1):
inv_shift_rows(state)
inv_sub_bytes(state)
add_round_key(state, round_keys[i])
inv_mix_columns(state)
# Run final round (skips the InvMixColumns step)
inv_shift_rows(state)
inv_sub_bytes(state)
add_round_key(state, round_keys[0])
# Convert state matrix to plaintext
plaintext = b''.join(bytes(row) for row in state)
return plaintext
print(decrypt(key, ciphertext))
Symmetric Starter
ECB Oracle
Source code for encryption:
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
KEY = ?
FLAG = ?
@chal.route('/ecb_oracle/encrypt/<plaintext>/')
def encrypt(plaintext):
plaintext = bytes.fromhex(plaintext)
padded = pad(plaintext + FLAG.encode(), 16)
cipher = AES.new(KEY, AES.MODE_ECB)
try:
encrypted = cipher.encrypt(padded)
except ValueError as e:
return {"error": str(e)}
return {"ciphertext": encrypted.hex()}
First, we try to find out how this encrypt function works.
I set the message to crypto{flag}, which is 12-byte long.
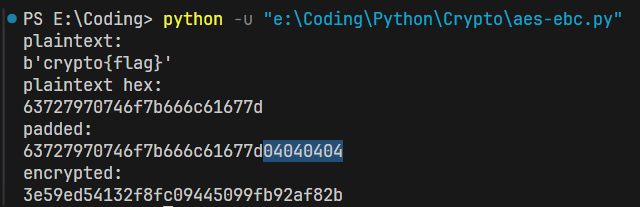
The padded text has the 04040404 part at the end, which means this plaintext is 4 bytes less than 16 bytes (the size of the block).
Try adding some random characters to the head of the message, and I find out that when adding enough 16 bytes, there’s one more block.
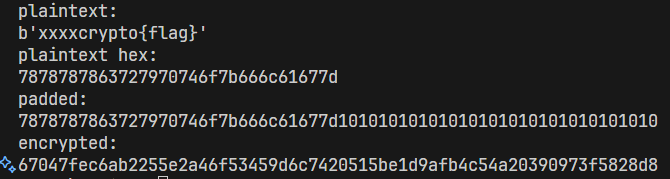
The padding bytes are 10101010101010101010101010101010 , which is 16 bytes long (full padding in a block).
Back to the source code provided: padded = pad(plaintext + FLAG.encode(), 16) and the interactive functionality on the website, when I try with a 6-byte-long input: aaaaaaaaaaaa The output is a 32-byte block. In another case, if I input a 7-byte-long string aaaaaaaaaaaaaa The output is a 48-byte block.
As we know from the local testing of the encrypting function, when the plaintext is 16-byte-long, there’s a full padding block added to the padded string.
So I can calculate that the length of the FLAG is 32 - 7 = 25 (bytes), because 25 bytes from the FLAG plus 7 bytes from the input is 32 bytes in total, “triggering” the encrypting function to add one more block.
That’s exactly 25 but not 26, because the encrypting function is special, when “touching” 32, the padding becomes 48 bytes instead of the full 32 bytes.
If the key length is 26 bytes, when we give a 6-byte-long input, the block size must be 48 bytes instead of 32 bytes.
Okay, now we have the length of FLAG is 25 bytes.
Let’s take a look at 2 cases of ciphertext:
aaaaaaaaaaaaaa (7 bytes)
aa64d8eb0053af1f48e3cb22f13ea76a
926b6882b9cd8bc87e1d7af1b6e86974
8399707d033badaa41663890fe57858e <- full padding
aaaaaaaaaaaaaaaa (8 bytes)
e78d824d901169322d2ace7e0cce69ba
f0bf605fee7dfaece5fc1be6bc5d2333
b0945df717a2ddd1314a8f0f93a716af
We can see that the last block of the second case is different from the last block of the first case (which is full of padding bytes).
The last character of the flag is } , so we can understand that this character is shifted to the last block.
aaaaaaaaaaaaaaaabbbbbbbbbbbbbbbb
bbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbb
}xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx
(b is the flag’s characters, x is padding bytes)
According to the padding rules, the padding bytes in this case should be 0f (less than 15 bytes when compared to 16).
So, I try with the input (plaintext as hex):
7d0f0f0f0f0f0f0f0f0f0f0f0f0f0f0f (16 bytes) (7d is hex form of })
Result:
aaaaaaaaaaaaaaaa
e78d824d901169322d2ace7e0cce69ba
f0bf605fee7dfaece5fc1be6bc5d2333
b0945df717a2ddd1314a8f0f93a716af
7d0f0f0f0f0f0f0f0f0f0f0f0f0f0f0f
b0945df717a2ddd1314a8f0f93a716af
75829521ed58d56e0acbf0641ddee18e
10501d0c4f881962fb6fd997db9ae87b
As we can see, the first block of the second ciphertext is the same as the last block of the first ciphertext, which is both the ciphertext of 7d0f0f0f0f0f0f0f0f0f0f0f0f0f0f0f
Now, we can find each byte of the flag by shifting each character to the last block.
First, testing with the last character of flag:
import requests
def get_request(param):
r = requests.get("https://aes.cryptohack.org/ecb_oracle/encrypt/" + param)
data = r.json()
return data['ciphertext']
byte_list = []
for i in range(1, 256):
b = hex(i)[2:]
if (len(b) == 1):
b = '0' + b
byte_list.append(b)
payload = 'AA' * 7 + 'AA'
ciphertext = get_request(payload)
last_block = ciphertext[-32:]
for b in byte_list:
inp = b + '0f' * 15
result = get_request(inp)
print('testing:' + inp)
first_block = result[:32]
if (first_block == last_block):
print('Found byte: ' + b)
break
Result:
It works correctly with the last character.
Let’s modify the code to brute-force the flag:
import requests
def get_request(param):
r = requests.get("https://aes.cryptohack.org/ecb_oracle/encrypt/" + param)
data = r.json()
return data['ciphertext']
byte_list = []
for i in range(1, 256):
b = hex(i)[2:]
if (len(b) == 1):
b = '0' + b
byte_list.append(b)
def get_padding(length):
return byte_list[length - 1]
offset = 'AA' * 7
payload = offset
pad_count = 15
flag = ''
blank_block = '8399707d033badaa41663890fe57858e'
while len(flag) < 32:
payload += 'AA'
ciphertext = get_request(payload)
last_block = ciphertext[-32:]
if (last_block == blank_block):
last_block = ciphertext[-64:-32]
pad_count = 16
for b in byte_list:
inp = b + flag + get_padding(pad_count) * pad_count
result = get_request(inp)
print('testing:' + inp)
first_block = result[:32]
if (first_block == last_block):
print('Found byte: ' + b)
flag = b + flag
break
pad_count -= 1
The code above gives the last 16 bytes of the flag. Result:

6e3675316e355f683437335f3363627d: n6u1n5_h473_3cb}
Now we need to recover the rest 9 bytes.
import requests
def get_request(param):
r = requests.get("https://aes.cryptohack.org/ecb_oracle/encrypt/" + param)
data = r.json()
return data['ciphertext']
byte_list = []
for i in range(1, 256):
b = hex(i)[2:]
if (len(b) == 1):
b = '0' + b
byte_list.append(b)
def get_padding(length):
return byte_list[length - 1]
offset = 'AA' * 7 + 'AA' * 16
payload = offset
pad_count = 15
flag = '6e3675316e355f683437335f3363627d'
blank_block = '8399707d033badaa41663890fe57858e'
while len(flag) < 50:
payload += 'AA'
ciphertext = get_request(payload)
last_block = ciphertext[-64:-32]
if (last_block == blank_block):
last_block = ciphertext[-64:-32]
pad_count = 16
for b in byte_list:
inp = b + flag + get_padding(pad_count) * pad_count
result = get_request(inp)
print('testing:' + inp)
first_block = result[:32]
if (first_block == last_block):
print('Found byte: ' + b)
flag = b + flag
break
pad_count -= 1
print('flag:' + bytes.fromhex(flag).decode())
Flag: crypto{p3n6u1n5_h473_3cb}
ECB CBC WTF
The difference between ECB and CBC is the correlation between blocks.
In AES mode ECB, the encrypting formular is:
But in AES mode CBC, the encrypting formular is:
→ Two similar plaintext blocks generate two different ciphertext blocks (because the blocks are different).
With , it will be taken in XOR operation with IV (initial vector).
Source code challenge:
from Crypto.Cipher import AES
KEY = ?
FLAG = ?
@chal.route('/ecbcbcwtf/decrypt/<ciphertext>/')
def decrypt(ciphertext):
ciphertext = bytes.fromhex(ciphertext)
cipher = AES.new(KEY, AES.MODE_ECB)
try:
decrypted = cipher.decrypt(ciphertext)
except ValueError as e:
return {"error": str(e)}
return {"plaintext": decrypted.hex()}
@chal.route('/ecbcbcwtf/encrypt_flag/')
def encrypt_flag():
iv = os.urandom(16)
cipher = AES.new(KEY, AES.MODE_CBC, iv)
encrypted = cipher.encrypt(FLAG.encode())
ciphertext = iv.hex() + encrypted.hex()
return {"ciphertext": ciphertext}